Introduction
Hello, world! 👋
My name is Marco and, after starting to prepare for coding interviews, I have decided to help you (and myself) by creating this website.
My aims are to:
- Explain the common algorithms and data structures used in the FAANG interviews.
- Explain which
Pythoncomponents to use in order to solve such problems. - Collect all the free resources to study a certain topic more in depth.
- Collect the solutions of some LeetCode problems. I will start with the famous Grind 75 list, and then add more problems based on your feedback.
If you are a novice, probably, this is not the best place to start with, but you can still use it later, once you are more familiar with coding interviews concepts.
Again, the main idea is to minimize the amount of time you would need to re-prepare for a new interview.
In fact, for those of you who do not know, typically, if one interview does not go well,
you would need to wait some time before re-applying for the same company.
The amount of time varies from company to company, but it can go from 6 months to 1 or more years.
If you do not practice enough during this period, you can lose all the progress you have made, and
you might also lose some internal brain connections that are allowing you to solve problems in no-time
(when you are well-trained).
At least, that's what I have experienced. You will surely not start from zero every time, but this website can help you to minimize the time you need to revise things you already know!
Contribute
Currently, the repository is still private, so, if you want to contribute or fix something, you can write me at mmicu.github00@gmail.com or join the public Discord channel.
Please, indicate if you want to be cited in the Contributors section.
If so, you can also provide your name and either one link (e.g. GitHub, X, etc.) or your email.
Support
As you might imagine, writing the content of this website required a lot of my spare time, plus, endless hours of reviews. As well as some money for the domain and other maintenance costs.
If you want so support me or just thank me, you can donate via Patreon or buy me a coffee.
Official Channels
Apart from the public Discord channel and private Discord one,
there is no social media I am using to advertise or communicate for algo-ds.com.
So, please, avoid using other communication sources and report them to me at mmicu.github00@gmail.com.
Additional Information
The website has been written by using the mdBook utility.
Moreover, all the Python code you see here is for version 3.8 and earlier,
which will impact the type hits.
This is because all the Python function signatures that you find in LeetCode have such notation.
In fact, we are going to use:
from typing import List
x: List[int] = [1, 2, 3]
Instead of:
x: list[int] = [1, 2, 3]
The latter is only available from Python >= 3.9.
Check this mypy type hints cheat sheet for more information.
Hidden code
It looks like the following snippet contains a single line of code.
However, if you go with your mouse over the snippets,
a couple of icons will appear at the top right.
The one with the eye symbol will allow you to show the hidden code:
s = "hello, world"
print(s)
Complexity Analysis
We can assess the efficiency of an algorithm in terms of space and time,
without actually running it and yet understand how slow/fast it is.
The complexity of an algorithm is denoted with the Big O notation, which describes the limiting behavior of a certain function when the argument tends to a particular value or infinity [1].
Classes of Functions
Before explaining how to measure the efficiency of an algorithm, we have to understand how to compare functions bounded to an input .
In fact, since both time and space complexities are expressed through mathematical functions, we need a way to compare them.
This chart [2] will help us:
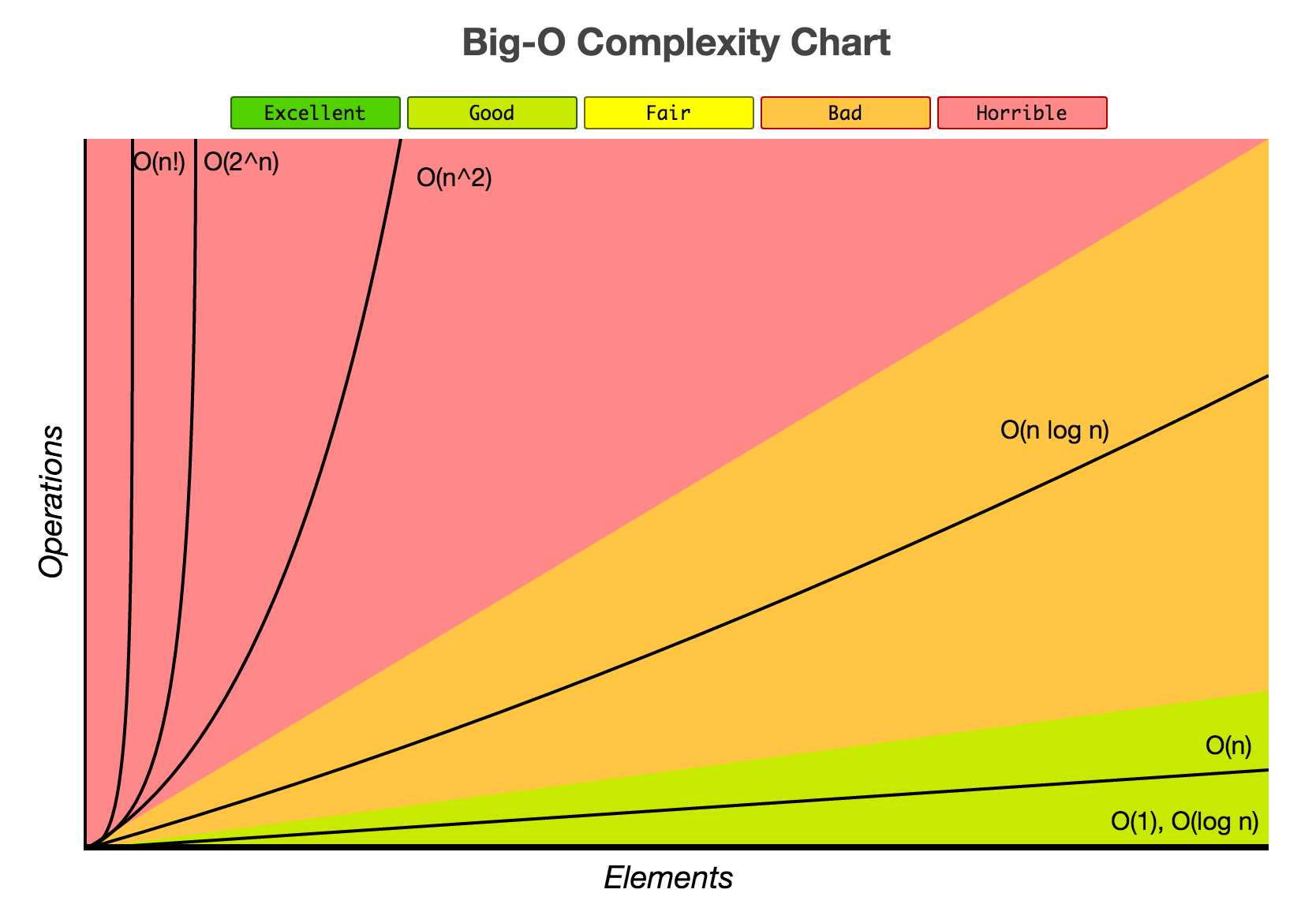
The importance of
You will likely found somewhere inside this notation (e.g. ), but is just the name of a variable. You can use any name you want, but, of course, is the most common to indicate the size of a certain input.
However, nothing prevents you to use other names. Just keep in mind that you have to pay attention on how you map the name of a certain variable to the inputs of your algorithm.
For example, you can use to map the size of a list. However, you could also use , , , or your preferred variable's name.
Common complexities
Before looking at some examples, remember that constant values are not considered. So, for example, and are both .
Moreover, we are also going to ignore terms with the lowest growth rate: is just .
Constant time
It is indicated with . Some examples:
# mathematical operations
a = 1
b = 2
c = a + b
# sets/hash-maps lookup
1 in s # where `s = {1, 2, 3}`
2 in map # where `m = {1: "one", 2: "two", 3: "three"}`
# pushing/popping from a stack
s = []
s.append(1)
s.append(2)
s.pop()
# enqueuing/dequeuing from a double-ended queue
from collections import deque
q = deque()
q.append(1)
q.append(2)
q.popleft()
Logarithmic time
It is indicated with . This is common for the Binary Search algorithm, and, more generally, whenever the search space is halved at each iteration.
Linear time
It is indicated with . This is probably the most common one, especially if the algorithm uses loops bounded to the size of the input.
The following are all algorithms.
Even with nested loops, we can still have such linear complexity.
Just be careful on the used variables.
nums: List[Any] = ... # a list took as input
# traverse a list (simplest case)
for num in nums:
print(num)
# two nested loop, but `m` is a constant
m = 2
for num in nums:
for _ in range(m):
print(num)
# two consecutive loops: `O(2 * n)`, hence `O(n)`
for num in nums:
print(num)
for num in nums:
print(num)
# ~
# find an element in a list. In the worst case, you need to traverse the entire list
target = 10
for num in nums:
if num == target:
print(f"Found the target `{target}`")
break
Logarithmic time with constant operations
It is indicated with , where is a constant factor.
You will usually encounter this complexity after applying a logarithmic algorithm for times.
Some examples are Binary Search and push/pop operations in a Heap.
Linearithmic time (Linear * Logarithmic)
It is indicated with .
You will usually encounter this complexity for sorting algorithms,
and divide and conquer ones.
Quadratic time
It is indicated with . Some examples:
# traverse a quadratic matrix
matrix: List[List[Any]] = ... # a quadratic matrix took as input
n = len(nums)
for i in range(n):
for j in range(n):
print(matrix[i][j])
# traverse a list twice
nums: List[Any] = ... # a list took as input
n = len(nums)
for i in range(n):
for j in range(i, n):
pass
Exponential time
It is indicated with . This usually appears in combinatorial problems. The best example is the recursive (non-optimized) Fibonacci sequence.
Factorial time
It is indicated with ,
where is equal to 1 * 2 * 3 * ... * n.
This usually appears in combinatorial problems.
You use this when you need to calculate all the permutations of a certain list.
References
Analyze Recursive Functions
The time complexity for recursive functions is the product between:
- The number of times the recursive function is called.
- The time complexity per call.
For the former, we can get help from the State Space, whereas for the latter we can simply use the technique I explained before.
The Space Tree
Based on the function we are examining, we can derive the space tree to understand the total number of calls.
Let's look at this example:
from typing import List
def print_list(lst: List[int]) -> None:
if not lst:
return
print(lst[0])
print_list(lst[1:])
lst = [1, 2, 3]
print_list(lst)
Which would give us the following space tree:
As you can see,
the number of nodes is proportional to the size of the input list, which is .
Therefore, the function will be called times (point 1) and the time complexity per call is (point 2).
In fact, we are simply printing a value, nothing else.
So, the final time complexity will be the product of such value, which is .
Regarding the space complexity,
we can use the Space Tree again,
which results in frames in the Call Stack,
so the space complexity is .
Other Examples
Fibonacci
A naive implementation of the Fibonacci sequence could be something like:
def fib(n: int) -> int:
if n == 0:
return 0
if n == 1 or n == 2:
return 1
return fib(n - 1) + fib(n - 2)
print(fib(4))
This would give us the following space tree:
We start from level 0 with 1 node,
then level 1 with 2 nodes, level 2 with 4 nodes - in general, nodes for the level.
So the time complexity will be .
Regarding the space, the maximum number of frames we would have is proportional to the height of the tree, which is at most . Hence, .
In fact, if we mark the nodes that would be in the call stack until we reach the first base case, we would have the following space tree:
Additional Resources
- Time Complexity Analysis by Abdul Bari.
- Chapter 2 of Competitive Programmer's Handbook by Antti Laaksonen.
The Complete Guide to Big O Notation & Complexity Analysis for Algorithmsby Alvin.- Big-O Notation - For Coding Interviews by NeetCode.
- Big O myths busted! by strager.
Conclusions
This is just an introduction to the Big O notation.
All the LeetCode solutions showed here contain information about
both space and time complexities.
However, if you still have some doubts and you want to enforce your theoretical understanding of this topic, you can take a look at the Additional Resources.
Arrays, Strings and Hashing
I have decided to group these three topics, because they are usually used together to solve a large range of problems.
Arrays
The static arrays used in other languages like C and C++ are not available in Python.
Instead, you can use dynamic ones, known by the list type:
>>> l = [1, 2, 3]
>>> len(l)
3
>>> for num in l:
... print(num)
...
1
2
3
>>> l.append(4) # [1, 2, 3, 4]
>>> l = [1, 2, "three"] # it can also contain mixed types
Operations
Let's check the complexity of the most common arrays' operations [1]:
| Operation | Time Complexity | Space Complexity | Syntax |
|---|---|---|---|
| Size | len(l) | ||
| Get i-th | l[i] | ||
| Set i-th | l[i] = val | ||
| Copy | [val for val in l] | ||
| Append | l.append(val) | ||
| Pop last | l.pop() | ||
| Pop i-th | l.pop(i) | ||
| Delete value | l.remove(val) | ||
| Iterate | for val in l: print(val) | ||
| Search | val in l | ||
| Minimum | min(l) | ||
| Maximum | max(l) |
Best Practices
Iterate over the list instead of using the index
# Good
for num in nums:
print(num)
# Not-so-good
for i in range(len(nums)):
print(nums[i])
Use enumerate
# Good
for i, num in enumerate(nums):
print(i, num)
# Not-so-good
for i in range(len(nums)):
print(i, nums[i])
Use enumerate and start argument
# Good
for i, num in enumerate(nums, start=1):
print(i, num)
# Not-so-good
for i, num in enumerate(nums):
print(i+1, num)
Use zip to iterate over multiple lists
# Good
for num_a, num_b, num_c in zip(lst_a, lst_b, lst_c):
print(num_a, num_b, num_c)
# Not-so-good
assert len(lst_a) == len(lst_b) == len(lst_c)
for i in range(len(lst_a)):
print(lst_a[i], lst_b[i], lst_c[i])
Use reversed for backward iteration
# Good
for num in reversed(nums):
print(num)
# Not-so-good
for i in range(len(nums) - 1, -1, -1):
print(nums[i])
References
Strings
Strings are immutable in Python,
which means that we cannot edit them.
In fact, the following code will throw an exception:
>>> s = "hello, world!"
>>> s[0] = "H"
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: 'str' object does not support item assignment
The solution is to use a list together with the join function to build up the string.
Notice that append takes and join takes ,
where is the number of elements in the list
(considering that each element is a string of length 1).
>>> lst = []
>>> lst.append("h")
>>> lst.append("e")
>>> lst.append("l")
>>> lst.append("l")
>>> lst.append("o")
>>> lst.append("!")
>>> print("".join(lst))
hello!
Operations
Check the ones for the Arrays.
Best Practices
Check the ones for the Arrays.
Hashing
Python includes two data types that use hashing internally to provide fast access to elements:
Sets and Dictionaries.
Sets
A set is an unordered collection with no duplicate elements [1].
>>> s = {1, 2, 3} # NOTE: for an empty set we must use `set()`. `{}` would initialize a `dict`
>>> 1 in s
True
>>> 4 in s
False
>>>
>>> s.add(4)
>>> 4 in s
True
>>> s.add(4) # `{1, 2, 3, 4}` no duplicates allowed as per definition
>>> s.remove(1) # {2, 3, 4}
>>> s.remove(1) # `KeyError: 1`
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
KeyError: 1
>>> s.discard(1) # it does not raise even if the element does not exist
Operations
Let's check the complexity of the sets' common operations [2]:
| Operation | Time Complexity | Space Complexity | Syntax |
|---|---|---|---|
| Add | s.add(val) | ||
| Size | len(s) | ||
| Search value | val in s | ||
| Delete value | s.remove(val) | ||
| Union | s | t | ||
| Intersection | s & t |
References
- [1]: https://docs.python.org/3/tutorial/datastructures.html#sets
- [2]: https://wiki.python.org/moin/TimeComplexity
Dictionaries
Dictionaries are also known as associative memories or associative arrays.
They are indexed by keys that can be any immutable type,
so strings and numbers can always be keys as well as tuples
(if they contain only strings, numbers, or tuples).
In fact, if a tuple contains any mutable object either directly or indirectly, it cannot be used as a key [1].
>>> d = {
... "a": 1,
... "b": 2,
... }
>>> "a" in d
True
>>> "c" in d
False
>>> d["e"] + 2
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
KeyError: 'e'
>>> d.get("e", 0) + 2 # use `get` to avoid `KeyError` and
# to use a default value for missing keys
>>> d["c"] = 3
>>> "c" in d
True
>>> d[[1, 2]] = 2 # cannot hash a `list` since it is *mutable*
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: unhashable type: 'list'
>>> d[(1, 2)] = 2 # a `tuple` is *immutable*, hence hashable
Operations
Let's check the complexity of dictionaries' common operations [2]:
| Operation | Time Complexity | Space Complexity | Syntax |
|---|---|---|---|
| Size | len(d) | ||
| Get item | d[k] or d.get(k) | ||
| Set item | d[k] = v | ||
| Delete item | del d[k] | ||
| Key in dict | k in d | ||
| Iterate | for k, v in d.items(): print(k, v) |
Best Practices
Use items()
# Good
for k, v in d.items():
print(f"{k} -> {v}")
# Not-so-good
for k in d:
print(f"{k} -> {d[k]}")
Use collections.defaultdict
# Good
from collections import defaultdict
d = defaultdict(int)
d["a"] += 1 # `defaultdict(<class 'int'>, {'a': 1})`
# ~
# Slightly better
d = {}
d["a"] = d.get("a", 0) + 1
# Not-so-good
d = {}
if "a" not in d:
d["a"] = 0
d["a"] += 1
# ~
Use collections.Counter
from collections import Counter
a = "abcabcz"
c = Counter(a) # Counter({'a': 2, 'b': 2, 'c': 2, 'z': 1})
c["a"] # 2
c["b"] # 2
c["c"] # 2
c["z"] # 1
c["x"] # 0
References
- [1]: https://docs.python.org/3/tutorial/datastructures.html#dictionaries
- [2]: https://wiki.python.org/moin/TimeComplexity
Two Pointers
The Two-pointers technique can be used to solve problems that involve arrays,
linked lists, or other sequences.
These sequences are not necessarily ordered, but, if so, you might need additional data structures to keep track of some information.
A Classic Example
Let's take Two Sum II - Input Array Is Sorted
as a classic example for a Two-pointers algorithm.
We surely need to take advantage of the fact that the array is ordered1.
If so, we can easily establish if the target cannot fit in the input.
Suppose a target of 10, with a list like [1, 2, 3, 4, 5].
Since the list is already ordered, we know that the elements at the positions i-1 and i-2 (last and second to last, respectively)
are the two highest values of the list (5 and 4 in our case).
The sum of the two values will not reach the target (9 < 10),
which means that no other sum between any two other values in the list can reach the target.
In fact, if the sum of the two highest values is less than the target, how can we find two other values big enough to reach the target? Well, we cannot since the list is ordered.
Then, how can we use such information?
Suppose that we start one pointer from the left and one from the right and we sum their values.
We will end up by summing up the minimum (element pointed by the left pointer) and
maximum (element pointed by the right pointer), having three possibilities:
nums[left] + nums[right] == target: we found the target, there's nothing else to do.nums[left] + nums[right] < target: the number we found is too small. So, summing up the current minimum and maximum is not enough. What can we do? Logically, we can simply find a new minimum and try with it, since the previous one was too small. We still need the current maximum as it is fundamental to find a target.nums[left] + nums[right] > target, which means that the number that we found is too big. In this case, the sum between the minimum and maximum is too big, so we can do the opposite: discard the current maximum by trying with a new one, and keep the current minimum.
The implementation would look something like:
from typing import List
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
left, right = 0, len(numbers) - 1
while left < right:
pointers_sum = numbers[left] + numbers[right]
if pointers_sum == target:
return [left + 1, right + 1]
if pointers_sum < target:
left += 1
else:
right -= 1
assert False, "Unreachable. Expected a single solution for the input."
Which has the following complexity:
- Time:
- Space:
Where n is the size of the list numbers.
-
This is one of the numerous questions we should always ask to the interviewer, especially about the inputs of the problem. Having an already sorted list as input can change the way we think of our algorithm a lot. ↩
Sliding Window
The Sliding Window Technique is a method used to efficiently solve problems
that involve processing subarrays or substrings within a larger sequence.
It operates by maintaining a window with either a static or a dynamic size, depending on the requirements of the problem.
The advantage of keeping such window is that we can drop
the time complexity from to .
In fact, a typical brute-force approach would require a double pass (hence ),
whereas a Sliding Window one can reduce it to a single one (hence ).
Let's now look at both the static and dynamic cases.
Sliding Window with a Static Size
Let's use Maximum Number of Vowels in a Substring of Given Length as our example.
A brute-force approach would consist of checking every substring of size starting at each character of the string, which is time complexity, where is the length of the string and is the length of the substring.
However, we can easily notice that we have a lot of repeated work.
In fact, what if we imagine to have a window of size k?
In this way, once we compute the window for the first time,
we can simply shrink it from the left and expand it to the right by one.
This -1 (shrinking) and +1 (expansion) would not change the size of the window,
which will remain k.
The implementation would look something like:
class Solution:
VOWELS = {"a", "e", "i", "o", "u"}
def maxVowels(self, s: str, k: int) -> int:
def is_vowel(char: str) -> bool:
assert isinstance(char, str)
assert len(char) == 1
return char in Solution.VOWELS
n = len(s)
assert k <= n
ans = 0
for right in range(k):
ans += int(is_vowel(s[right]))
left = 0
win_res = ans
for right in range(right + 1, n):
win_res -= int(is_vowel(s[left]))
win_res += int(is_vowel(s[right]))
left += 1
ans = max(ans, win_res)
return ans
Which has the following complexity:
- Time:
- Space:
Where n is the size of the string s.
Sliding Window with a Dynamic Size
Let's use Longest Substring Without Repeating Characters as our example.
A brute-force approach would consist in checking every substring and stop as soon as we find a duplicated characters. We have a total of substrings and we would require to look for duplicated characters. So our total time complexity would be , where is the length of the string.
In this case, we do not have an explicit window of a certain size as for the previous example. However, we can still apply a sliding window algorithm.
In fact, suppose that we do not have repeated characters in the input string: the window will be the entire string itself.
Now, let's suppose to have an example like abcdaefghi.
Here, a is the duplicated character, which is at positions 0 and 4.
We can build a window from the first a till the second one,
then, we can shrink the window till the a is not repeated anymore,
which means that the window will start from b to a (1 till 4).
Lastly, we can continue increasing our window till the end,
since we do not have other duplicated characters.
The implementation would look something like:
from typing import Set
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
chars: Set[str] = set()
ans = left = 0
for right, char in enumerate(s):
while char in chars:
chars.remove(s[left])
left += 1
chars.add(char)
win_size = right - left + 1
ans = max(ans, win_size)
return ans
Which has the following complexity:
- Time:
- Space:
Where is the size of the string and is the number of distinct characters in the string .
Binary Search
Binary Search is an efficient algorithm used to find a target value within a sorted array.
In each iteration, it halves the search space, achieving logarithmic time complexity ().
Implementation
We can implement this algorithm both recursively and iteratively.
Iterative Binary Search
from typing import List
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
if nums[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
Recursive Binary Search
from typing import List
class Solution:
def search(self, nums: List[int], target: int) -> int:
def helper(low: int, high: int) -> int:
if low > high:
return -1
mid = (low + high) // 2
if nums[mid] == target:
return mid
if nums[mid] < target:
return helper(mid + 1, high)
else:
return helper(low, mid - 1)
return helper(0, len(nums) - 1)
bisect module
In Python, we can use the bisect module
to look for the insertion point (either left or right) in sorted lists.
These are the signatures of the two functions:
bisect.bisect_left(a, x, lo=0, hi=len(a), *, key=None)bisect.bisect_right(a, x, lo=0, hi=len(a), *, key=None)
Let's have a look at the following examples:
>>> import bisect
>>> l = [0, 0, 1, 1, 1, 2, 3, 4, 4]
>>> len(l)
9
# no values less than `-100`. Hence, it would be the first element of the list
>>> bisect.bisect_left(l, -100)
0
# smaller value is `0`. Hence, `0` goes first for `bisect_left`
>>> bisect.bisect_left(l, 0)
0
# smaller value is `0`, which is already at position `0` and `1`.
# Hence, the next `0` would go at position `2` for `bisect_right`
>>> bisect.bisect_right(l, 0)
2
# same considerations for the `0` for another existing element in the list
>>> bisect.bisect_left(l, 4)
7
>>> bisect.bisect_right(l, 4)
9
>>>
# no element bigger than `100`. Hence, it will be the new last element of the list
>>> bisect.bisect_right(l, 100)
9
Notice that in the examples above
we always used 0 and len(l) as lower and upper bounds, respectively.
However, we can also specify any other range.
Additional Usage
Binary Search works quite well on any sorted sequence.
So let's now think of an ordered list of booleans:
l = [False, False, False, False, True, True]
It is easy to determine the first False value of the list, since it is ordered.
However, what about the first True value?
Again, the list is ordered, which means that we can apply Binary Search:
from typing import List
def search(self, nums: List[int]) -> int:
left, right = 0, len(nums) - 1
first_true_idx = -1
while left <= right:
mid = (left + right) // 2
if nums[mid]:
first_true_idx = mid
right = mid - 1
else:
left = mid + 1
return first_true_idx
first_true_idx will contain the index of the leftmost True value of the list.
How can we use such pattern?
Suppose that we have a monotonic increasing function:
def mon_inc_func(n):
return n > 2
For the following input, the function will return an ordered output:
input = [0, 1, 2, 3, 4, 5, 6]
output = [mon_inc_func(i) for i in input]
print(output)
# [False, False, False, True, True, True, True]
Now, suppose that we do not know how this monotonic increasing function is implemented,
so we do not know the source code of mon_inc_func.
How can we use Binary Search to find the first value of the function that returns True?
We can use the previous snippet and simply replace nums[mid], which is looking for a True value, with the result of the function:
from typing import List
def unknown_function(n: int) -> bool:
pass
def search(self, nums: List[int]) -> int:
left, right = 0, len(nums) - 1
first_true_idx = -1
while left <= right:
mid = (left + right) // 2
if unknown_function(mid): # instead of `nums[mid]`
first_true_idx = mid
right = mid - 1
else:
left = mid + 1
return first_true_idx
Monotonic Function Example
Let's look at a real example,
where we can apply this variation of Binary Search.
We can use the First Bad Version problem.
Linked Lists
Linked Lists are a linear data structures consisting of nodes,
each containing a value and a reference to the next node.
Unlike arrays, linked lists allow an efficient insertion and deletion.
However, we cannot access elements by index, so we need to traverse the entire list to do so.
Operations
Let's check the complexity of linked lists' common operations:
| Operation | Time Complexity | Space Complexity |
|---|---|---|
| Size | ||
| Get i-th | ||
| Set i-th | ||
| Copy | ||
| Append | ||
| Pop first | ||
| Pop last | ||
| Pop i-th | ||
| Delete value | ||
| Iterate | ||
| Search |
Types
There are two kinds of Linked Lists:
collections.deque
The deque module can also simulate a Linked List.
You can find more information in the Queue paragraph.
Singly Linked Lists
Let's use Design Linked List to design our Singly Linked List.
from typing import Generic, Optional, TypeVar
T = TypeVar("T")
class ListNode(Generic[T]):
def __init__(self, val: T, next_ptr: Optional["ListNode"] = None) -> None:
self.val = val
self.next = next_ptr
class MyLinkedList:
def __init__(self):
self.size = 0
self.head = ListNode(-1)
def get(self, index: int) -> int:
if index < 0 or index >= self.size:
return -1
return self._getNodeAtIndex(index + 1).val
def addAtHead(self, val: int) -> None:
self.addAtIndex(0, val)
def addAtTail(self, val: int) -> None:
self.addAtIndex(self.size, val)
def addAtIndex(self, index: int, val: int) -> None:
if index < 0 or index > self.size:
return
p = self._getNodeAtIndex(index)
node = ListNode(val)
node.next = p.next
p.next = node
self.size += 1
def deleteAtIndex(self, index: int) -> None:
if index < 0 or index >= self.size:
return
p = self._getNodeAtIndex(index)
p.next = p.next.next
self.size -= 1
def _getNodeAtIndex(self, index: int) -> ListNode[int]:
p = self.head
for _ in range(index):
p = p.next
return p
The key idea here is to use a dummy head node to avoid to write a lot of code,
which would be used to check the validity of the head itself.
Except for addAtHead, which is for the time complexity,
all the other operations are .
The space complexity is for each operation,
however, after operations we might end up having a list of elements
(assuming that they are all valid consecutive insert operations).
Doubly Linked Lists
Let's use Design Linked List to design our Doubly Linked List.
from typing import Generic, Optional, TypeVar
T = TypeVar("T")
class ListNode(Generic[T]):
def __init__(
self,
val: T,
prev_ptr: Optional["ListNode"] = None,
next_ptr: Optional["ListNode"] = None,
) -> None:
self.val = val
self.prev = prev_ptr
self.next = next_ptr
class MyLinkedList:
def __init__(self):
self.size = 0
self.head = ListNode(-1)
self.tail = ListNode(-1)
self.head.next = self.tail
self.tail.prev = self.head
def get(self, index: int) -> int:
if index < 0 or index >= self.size:
return -1
return self._getNodeAtIndex(index + 1).val
def addAtHead(self, val: int) -> None:
self.addAtIndex(0, val)
def addAtTail(self, val: int) -> None:
self.addAtIndex(self.size, val)
def addAtIndex(self, index: int, val: int) -> None:
if index < 0 or index > self.size:
return
p = self._getNodeAtIndex(index)
n = p.next
node = ListNode(val)
node.prev = p
node.next = n
p.next = node
n.prev = node
self.size += 1
def deleteAtIndex(self, index: int) -> None:
if index < 0 or index >= self.size:
return
p = self._getNodeAtIndex(index)
n = p.next.next
p.next = n
n.prev = p
self.size -= 1
def _getNodeAtIndex(self, index: int) -> ListNode[int]:
p = self.head
for _ in range(index):
p = p.next
return p
As for the Singly Linked List,
besides the dummy head node we need the dummy tail as well.
For the same reason,
we can use such nodes to avoid to write code to handle edge cases.
Except for addAtHead, which is for the time complexity,
all the other operations are .
The space complexity is for each operation,
however, after operations we might end up having a list of elements
(assuming that they are all valid consecutive insert operations).
Stacks and Queues
Stacks and Queues can be used as auxiliary data structures to solve
a large set of problems.
Usually, you can use them while iterating over a sequence to store intermediate values that you can use later to compute some results.
Although very similar, there are a few differences between the two:
Stacksfollow theLIFOprinciple, which meansLast In First Out. The last element added (push) to the stack will be the first one to be removed (pop). A classic example that I remember from high school (a long time ago 🥲) is the stack of plates: if you add one at the top, you have to remove it first, before reaching the ones at the bottom.Queuesfollow theFIFOprinciple, which meansFirst In First Out. The first element added (enqueue) to the queue will be the the first one to be removed (dequeue). Think of a queue at the post office: the first person who arrives will be served first.
The deque object
Before discussing about the Python usage of these two data structures,
let me introduce the deque object from the collections container.
Deques (pronounced deck) is a generalization of Stacks and Queues and
it represents a Double-ended Queue [1].
This object can be used to for both Stacks and Queues.
References
Stacks in Python
A standard data type list can be used as a Stack in Python:
>>> s = []
>>> s.append(1)
>>> s.append(2)
>>> s.append(3)
>>> s.pop()
3
>>> s.pop()
2
>>> s
[1]
>>> len(s)
1
>>> s[-1] # top of the stack
1
Both append and pop are ,
whereas looking for an element is , where is the size of the stack.
The deque can be used as well (even if I prefer the standard list).
You can also notice that the methods are actually the same and
only the initialization is different:
>>> from collections import deque
>>> s = deque()
>>> s.append("a")
>>> s.append("b")
>>> s.pop()
'b'
>>> s
deque(['a'])
>>> len(s)
1
>>> s[-1]
'a'
Queues in Python
The deque object we discussed about before can be also used to represent a normal Queue.
The usual enqueuing and dequeuing can be done by using the methods append and popleft, respectively.
>>> from collections import deque
>>> q = deque()
>>> q.append(1)
>>> q.append(2)
>>> q.append(3)
>>> q.append(4)
>>> q.popleft()
1
>>> q.popleft()
2
>>> q
deque([3, 4])
>>> len(q)
2
>>> q[0]
3
>>> q[-1]
4
Both append and popleft are ,
whereas looking for an element is , where is the size of the queue.
Monotonic Stacks and Queues
As described in the Introduction, we can use a stack as an auxiliary data structure to solve problems and improve overall time complexity.
Let's use Daily Temperatures as our example.
A brute force approach would consist of checking every possible temperature:
from typing import List
class Solution:
def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
n = len(temperatures)
res = [0] * len(temperatures)
for i in range(n):
for j in range(i + 1, n):
t1 = temperatures[i]
t2 = temperatures[j]
if t1 < t2:
res[i] = j - i
break
return res
Which has the following complexity:
- Time:
- Space:
Where is the size of the temperatures list.
Can we do better? Of course, yes.
Suppose to have an increasing sequence like [1, 2, 3, 4, 5].
The result would be [1, 1, 1, 1, 0].
In fact, the i-th temperature is always less compared to the i+1 one,
except for the last one, which has no higher value.
Another example could be [1, 1, 1, 1, 100].
The corresponding result would be [4, 3, 2, 1, 0].
This example suggests that the last value is the target value for all.
So we could start from the last position and keep a monotonic increasing stack to keep track of the temperatures. In this way, the stack will contain a list of possible candidates for our target temperature.
For example, for [100, 30, 40, 50, 60, 200] we can notice that once we process the first element,
the stack is:
30
40
50
60
200
In fact, since we iterate backward, we will process the first element in the last iteration. At this point, we can pop from the stack until we find a higher temperature.
Lastly, to calculate the actual distance, we also need to store the index of the i-th temperature.
So, the previous stack would look something like:
(30, 1)
(40, 2)
(50, 3)
(60, 4)
(200, 5)
The optimal solution is:
from typing import List, Tuple
class Solution:
def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
n = len(temperatures)
res = [0] * len(temperatures)
stack: List[Tuple[int, int]] = []
for i in range(n - 1, -1, -1):
temperature = temperatures[i]
while stack and stack[-1][0] <= temperature:
stack.pop()
if stack:
res[i] = stack[-1][1] - i
stack.append((temperature, i))
return res
Which has the following complexity:
- Time:
- Space:
Where is the size of the temperatures list.
Trees
A Tree is a Connected Acyclic Graph.
We will study the Graphs later,
so don't worry if you do not get it immediately.
A n-ary tree is a Tree in which each node contains at most n children.
The most common one is the Binary Tree,
where each node has at most 2 children ().
As for the Linked Lists, there is no Python data type for trees.
However, we can easily define a Binary one:
from typing import Generic, Optional, TypeVar
T = TypeVar("T")
class TreeNode(Generic[T]):
def __init__(
self,
val: T,
left: Optional["TreeNode"] = None,
right: Optional["TreeNode"] = None,
) -> None:
self.val = val
self.left = left
self.right = right
Or a n-ary tree:
from typing import Generic, List, Optional, TypeVar
T = TypeVar("T")
class TreeNode(Generic[T]):
def __init__(self, val: T, children: Optional[List["TreeNode"]] = None) -> None:
self.val = val
self.children = [] if not children else children
Terminology
These are the most common terms associated to a Tree [1]:
- Root: node with no incoming edges.
- Children: nodes with some incoming edges.
- Sibling: nodes having the same parent.
- Leaf: nodes with no children.
- Height: number of edges between node
AandB.
Types of Binary Trees
Full Binary Tree
A Full Binary Tree has either zero or two children.
Complete Binary Tree
A Complete Binary Tree has all levels filled except the last one,
which is filled from left to right.
Perfect Binary Tree
A Perfect Binary Tree has every internal node with two children and
all the leaf nodes are at the same level.
This type of tree has exactly nodes, where is the height of the tree.
In this case, , hence nodes.
References
Tree Traversal
Breadth-First Search (BFS) and Depth-First Search (DFS) can both be used to traverse a tree.
The two algorithms run in for both time and space,
where is the number of nodes in the tree.
DFS for Trees
There are three ways of traversing a tree by using a DFS approach,
and these can be done both iteratively and recursively.
Pre-order traversal
The traversal order is:
- Node.
- Left.
- Right.
The iterative and recursive solutions can be tested in LeetCode.
from typing import List, Optional
class TreeNode:
def __init__(self, val,
left: Optional['TreeNode'] = None,
right: Optional['TreeNode'] = None) -> None:
self.val = val
self.left = left
self.right = right
from typing import List, Optional
class Solution:
def preorderTraversal(self, root: Optional[TreeNode] = None) -> List[int]:
def dfs(node: Optional[TreeNode] = None) -> None:
if not node:
return
nonlocal res
res.append(node.val)
for child in [node.left, node.right]:
dfs(child)
res = []
dfs(root)
return res
from typing import List, Optional
class TreeNode:
def __init__(self, val,
left: Optional['TreeNode'] = None,
right: Optional['TreeNode'] = None) -> None:
self.val = val
self.left = left
self.right = right
from typing import List, Optional
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
res = []
stack = [root]
while stack:
node = stack.pop()
res.append(node.val)
for child in [node.right, node.left]:
if child:
stack.append(child)
return res
In-order traversal
The traversal order is:
- Left.
- Node.
- Right.
The iterative and recursive solutions can be tested in LeetCode.
from typing import List, Optional
class TreeNode:
def __init__(self, val,
left: Optional['TreeNode'] = None,
right: Optional['TreeNode'] = None) -> None:
self.val = val
self.left = left
self.right = right
from typing import List, Optional
class Solution:
def inorderTraversal(self, root: Optional[TreeNode] = None) -> List[int]:
def dfs(node: Optional[TreeNode] = None) -> None:
if not node:
return
dfs(node.left)
nonlocal res
res.append(node.val)
dfs(node.right)
res = []
dfs(root)
return res
from typing import List, Optional
class TreeNode:
def __init__(self, val,
left: Optional['TreeNode'] = None,
right: Optional['TreeNode'] = None) -> None:
self.val = val
self.left = left
self.right = right
from typing import List, Optional
class Solution:
def inorderTraversal(self, root: Optional[TreeNode] = None) -> List[int]:
if not root:
return []
res = []
stack = [root]
while stack:
node = stack.pop()
while node:
stack.append(node)
node = node.left
if stack:
node = stack.pop()
res.append(node.val)
stack.append(node.right)
return res
Post-order traversal
The traversal order is:
- Left.
- Right.
- Node.
The iterative and recursive solutions can be tested in LeetCode.
from typing import List, Optional
class TreeNode:
def __init__(self, val,
left: Optional['TreeNode'] = None,
right: Optional['TreeNode'] = None) -> None:
self.val = val
self.left = left
self.right = right
from typing import List, Optional
class Solution:
def postorderTraversal(self, root: Optional[TreeNode] = None) -> List[int]:
def dfs(node: Optional[TreeNode] = None) -> None:
if not node:
return
dfs(node.left)
dfs(node.right)
nonlocal res
res.append(node.val)
res = []
dfs(root)
return res
from typing import List, Optional
class TreeNode:
def __init__(self, val,
left: Optional['TreeNode'] = None,
right: Optional['TreeNode'] = None) -> None:
self.val = val
self.left = left
self.right = right
from typing import List, Optional
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
res = []
# Each element of stack is a tuple: (node, visited_flag)
stack = [(root, False)]
while stack:
node, visited = stack.pop()
if visited:
res.append(node.val)
else:
stack.append((node, True))
for child in [node.right, node.left]:
if child:
stack.append((child, False))
return res
BFS for Trees
The BFS algorithm uses a queue to process all the nodes level-by-level in a tree:
from typing import List, Optional
class TreeNode:
def __init__(self, val,
left: Optional['TreeNode'] = None,
right: Optional['TreeNode'] = None) -> None:
self.val = val
self.left = left
self.right = right
from collections import deque
from typing import Deque, List, Optional
class Solution:
def levelOrder(self, root: Optional[TreeNode] = None) -> List[List[int]]:
res = []
queue: Deque[int] = deque([])
if root:
queue.append(root)
while queue:
res_level = []
for _ in range(len(queue)):
node = queue.popleft()
res_level.append(node.val)
for child in [node.left, node.right]:
if child:
queue.append(child)
res.append(res_level)
return res
The DFS algorithm can also be used for a level-by-level traversal, even if it is less intuitive than using a queue:
from typing import List, Optional
class TreeNode:
def __init__(self, val,
left: Optional['TreeNode'] = None,
right: Optional['TreeNode'] = None) -> None:
self.val = val
self.left = left
self.right = right
from typing import List, Optional
class Solution:
def levelOrder(self, root: Optional[TreeNode] = None) -> List[List[int]]:
def dfs(level: int, node: Optional[TreeNode] = None) -> None:
if not node:
return
nonlocal res
if len(res) == level:
res.append([])
res[level].append(node.val)
for child in [node.left, node.right]:
if child:
dfs(level + 1, child)
res = []
dfs(0, root)
return res
Both solutions can be tested in LeetCode.
Binary Search Tree (BST)
A Binary Search Tree is a type of Binary Tree,
where each node has a value greater than all nodes in its left subtree and less than all nodes in its right subtree.
This applies to all nodes in the tree.
Compared to a standard Binary Tree,
a BST has a logarithmic time complexity for searching, inserting and deleting.
This is true if the BST is balanced.
In fact, for an unbalanced one,
we are going to have a linear time complexity as for a normal Binary Tree.
Trie (Prefix Tree)
A Trie (pronounced as try), also known as Prefix Tree, is a Tree data structure that is used to efficiently store and locate strings with a predefined set.
As the same suggest, we can store prefixes to avoid to store common strings more than once.
For example, suppose that we have the following strings:
strings = [
"tab",
"table",
"tank",
"tart",
"task",
]
We can notice that all of them share the same prefix ta.
So, we could use a tree to store these single characters and
avoid to duplicate them.
Lastly, we can have a flag to mark a complete word (green node).
In this way,
we can distinguish between a normal character and a character that forms an actual string.
Implementation
You can implement this data structure by using a n-ary tree.
from typing import Dict, Optional
class TrieNode:
def __init__(self, is_word: Optional[bool] = False) -> None:
self.children: Dict[str, "TrieNode"] = {}
self.is_word = is_word
class Trie:
def __init__(self) -> None:
self.head = TrieNode()
def insert(self, word: str) -> None:
p = self.head
for char in word:
if char not in p.children:
p.children[char] = TrieNode()
p = p.children[char]
p.is_word = True
def search(self, word: str) -> bool:
return self._contains(word=word, match_word=True)
def startsWith(self, prefix: str) -> bool:
return self._contains(word=prefix, match_word=False)
def _contains(self, word: str, match_word: bool) -> bool:
p = self.head
for char in word:
if char not in p.children:
return False
p = p.children[char]
return p.is_word if match_word else True
Operations
Let's check the complexity for the three Trie operations:
insert:- Time: .
- Space: .
search:- Time: .
- Space: .
startsWith:- Time: .
- Space: .
Where is the size of the word and is the size of the prefix.
Graphs
A Graph is a collection of Vertices/Nodes (denoted as ) and
Edges (denoted as ) that connect pairs of vertices.
If the Edges have a direction, then we have a Directed Graph:
Otherwise, we have an Undirected Graph:
For both graphs, the nodes are a, b, c and d.
However, the edges differ between the two.
In fact, if we group the edges for the single nodes,
we would have the following ones for the Directed graph:
a -> {b, c}
b -> {d}
c -> {d}
d -> {}
And these for the Undirected one:
a -> {b, c}
b -> {a, d}
c -> {a, d}
d -> {b, c}
So, we simply mapped the nodes with a list of so called Neighbors.
Connected and Disconnected Graphs
The previous Graphs were all Connected,
since there was a path between each Node.
However, we can also have Disconnected ones:
In this case,
there is no connection between the nodes a, b and c, d.
Representation
The most common way to represent a Graph is within an Adjacency List,
which can be a Python dictionary that maps the Node to the set of Neighbors.
Usually, a list of Edges is provided,
where each element is either a list or a tuple of two elements.
For example:
edges = [
["a", "b"],
["a", "c"],
]
Adjacency List for a Directed Graph
Since the Graph is Directed,
we just need to consider a single dependency between two nodes (a single add call).
from collections import defaultdict
edges = [
("a", "b"),
("a", "c"),
]
graph = defaultdict(list)
for a, b in edges:
graph[a].append(b)
Adjacency List for an Undirected Graph
For the Undirected one,
we need a double dependency between the two nodes.
In fact, node a has b as Neighbor, and vice versa.
from collections import defaultdict
edges = [
("a", "b"),
("a", "c"),
]
graph = defaultdict(list)
for a, b in edges:
graph[a].append(b)
graph[b].append(a) # the only difference compared to the other implementation
Graph Traversal
As for Trees,
we can traverse a Graph by using DFS or BFS.
The complexity of the two algorithms is for both time and space, where:
In fact, we need time to build the Adjacency List and
time to push and pop elements to and from the stack, respectively.
Regarding the space,
we need to store edges in the dictionary and Vertices/Nodes in the set.
DFS for Graphs
Let's apply a DFS algorithm to an actual problem,
like Find if Path Exists in Graph.
The first thing to do is to understand which kind of Graph we have to build.
The problem clearly specifies that we have a bi-directional graph,
which means that the Graph is Undirected.
Now, we can build the actual Graph.
In fact, only a list of Edges was provided,
which is not a good data structure to use for representing it.
So, let's apply the same approach explained before to build the Adjacency List.
We can either use a Recursive or Iterative approach to perform a DFS traversal to the Graph.
You can notice that the code is very similar to the DFS Tree Traversal one.
The only difference is in the way you get the adjacent nodes.
For a Binary Tree you have the left and right children
(or a list of children for a n-ary Tree),
whereas for a Graph you have a sequence of Neighbors.
Moreover, especially for the Directed Graphs,
we need to keep a set of visited Nodes to avoid to revisit a Node.
For a Tree we do not have such problem,
since we cannot go back to the parent node from its children.
This is the Recursive approach:
from collections import defaultdict
from typing import DefaultDict, List, Set
class Solution:
def validPath(
self, n: int, edges: List[List[int]], source: int, destination: int
) -> bool:
graph = self.buildAdjacencyList(edges)
return self.dfs(graph, source, destination, set())
def dfs(
self, graph: DefaultDict[int, List], source: int, destination: int, visited: Set
) -> bool:
if source in visited:
return False
if source == destination:
return True
visited.add(source)
for neighbor in graph[source]:
if self.dfs(graph, neighbor, destination, visited):
return True
return False
def buildAdjacencyList(self, edges: List[List[int]]) -> DefaultDict[int, List]:
graph = defaultdict(list)
for a, b in edges:
graph[a].append(b)
graph[b].append(a)
return graph
And this is the Iterative one.
As usual, we can use a Stack to emulate the recursive calls.
from collections import defaultdict
from typing import DefaultDict, List
class Solution:
def validPath(
self, n: int, edges: List[List[int]], source: int, destination: int
) -> bool:
graph = self.buildAdjacencyList(edges)
return self.dfs(graph, source, destination)
def dfs(self, graph: DefaultDict[int, List], source: int, destination: int) -> bool:
visited = {source}
nodes = [source]
while nodes:
node = nodes.pop()
if node == destination:
return True
for neighbor in graph[node]:
if neighbor not in visited:
nodes.append(neighbor)
visited.add(neighbor)
return False
def buildAdjacencyList(self, edges: List[List[int]]) -> DefaultDict[int, List]:
graph = defaultdict(list)
for a, b in edges:
graph[a].append(b)
graph[b].append(a)
return graph
BFS for Graphs
The same assumptions made for the DFS approach apply here too. Here is a summary:
- Identify the type of the
Graph. - Build the
Adjacency List. - For
Directed Graphs, keep avisitedset to avoid to revisitNodes.
As for Trees, let's use a Queue to implement the BFS algorithm.
from collections import defaultdict, deque
from typing import DefaultDict, List
class Solution:
def validPath(
self, n: int, edges: List[List[int]], source: int, destination: int
) -> bool:
graph = self.buildAdjacencyList(edges)
return self.bfs(graph, source, destination)
def bfs(self, graph: DefaultDict[int, List], source: int, destination: int) -> bool:
visited = {source}
nodes = deque([source])
while nodes:
node = nodes.popleft()
if node == destination:
return True
for neighbor in graph[node]:
if neighbor not in visited:
nodes.append(neighbor)
visited.add(neighbor)
return False
def buildAdjacencyList(self, edges: List[List[int]]) -> DefaultDict[int, List]:
graph = defaultdict(list)
for a, b in edges:
graph[a].append(b)
graph[b].append(a)
return graph
Disjoint Sets (Union-Find)
A Disjoint Set (also known as a Union-Find data structure) is a data structure that stores a collection of disjoint (non-overlapping) Sets [1].
For example:
In this case,
we have a total of 3 Disjoint Sets:
- {0, 1}.
- {2, 3, 4}.
- {5}.
From now on, let's only use Union Find.
Common Operations
A Union Find data structure allows two main operations:
- union(a, b): merge the sets to which the nodes
aandbbelong. - find(a): determine the set for the node
a.
Implementation
There are two ways1 to implement Union Find.
The complexities below refer to the Time.
For the Space,
we need to build a list of n nodes to contain information about the nodes,
hence it will always be .
- Quick Find:
- for
findoperation. - for
unionoperation.
- for
- Quick Union.
-
findoperation. -
unionoperation.
-
At a first look,
Quick Find seems better,
but there are several Quick Union optimization techniques we can use
to drastically reduce the overall complexity.
We are going to use Find if Path Exists in Graph problem to apply such data structures.
References
-
It is also common to have a third operation, which takes two nodes as input and return
Trueif they belong to the same set, otherwiseFalse. ↩
Quick Find
For this kind of implementation, we store the root vertexes of each node.
For example:
Would have the following values:
index : 0 1 2 3 4 5
value (root node) : [0 0 0 3 3 3]
Implementation
The implementation would look something like:
class UnionFind:
def __init__(self, n: int) -> None:
self.n = n
self.roots = [i for i in range(self.n)]
def union(self, a: int, b: int) -> None:
self._validate(a)
self._validate(b)
root_a = self.find(a)
root_b = self.find(b)
if root_a == root_b:
return
for i, root in enumerate(self.roots):
if root == root_b:
self.roots[i] = root_a
def find(self, a: int) -> int:
return self.roots[a]
def connected(self, a: int, b: int) -> bool:
return self.find(a) == self.find(b)
def _validate(self, a: int) -> None:
assert 0 <= a < self.n
Usage
As explained earlier, let's apply the following data structure to Find if Path Exists in Graph.
from typing import List
class Solution:
def validPath(
self, n: int, edges: List[List[int]], source: int, destination: int
) -> bool:
union_find = self.build_disjoint_set(n, edges)
return union_find.connected(source, destination)
def build_disjoint_set(self, n: int, edges: List[List[int]]) -> UnionFind:
union_find = UnionFind(n)
for a, b in edges:
union_find.union(a, b)
return union_find
Although this implementation is valid,
we will get a Time Limit Exceeded for this problem.
Quick Union
For this kind of implementation, we store the parent vertexes of each node.
For example:
Would have the following values:
index : 0 1 2 3 4 5
value (root node) : [0 0 1 3 3 4]
Implementation
The implementation would look something like:
class UnionFind:
def __init__(self, n: int) -> None:
self.n = n
self.parents = [i for i in range(self.n)]
def union(self, a: int, b: int) -> None:
self._validate(a)
self._validate(b)
parent_a = self.find(a)
parent_b = self.find(b)
if parent_a != parent_b:
self.parents[parent_b] = parent_a
def find(self, a: int) -> int:
while a != self.parents[a]:
a = self.parents[a]
return a
def connected(self, a: int, b: int) -> bool:
return self.find(a) == self.find(b)
def _validate(self, a: int) -> None:
assert 0 <= a < self.n
Usage
Compared to the Quick Find,
we have passed more test cases in
Find if Path Exists in Graph,
but this is not enough.
We are still getting a Time Limit Exceeded.
from typing import List
class Solution:
def validPath(
self, n: int, edges: List[List[int]], source: int, destination: int
) -> bool:
union_find = self.build_disjoint_set(n, edges)
return union_find.connected(source, destination)
def build_disjoint_set(self, n: int, edges: List[List[int]]) -> UnionFind:
union_find = UnionFind(n)
for a, b in edges:
union_find.union(a, b)
return union_find
Union by Rank in Quick Union
The Union by Rank is an optimization technique
that can be applied to the Quick Union implementation.
In the previous implementations of Quick Find and Quick Union,
we always chose the first node as the dominant one.
However, this could lead to a skewed list of nodes, which looks like a Linked List. As we know, for this data structure the time complexity to find an element is . Therefore, the same applies here.
Instead, we could use the highest height of the set that belongs to either node a or b to
choose the root node.
Now you might ask: why should we select the highest height?
Let's look at an example:
If you want to union 1 and 4,
you will end up having two possible scenarios.
After calculating the parent nodes of 1 and 4,
which are 0 and 4, respectively,
we could build a set with 0 (height is 3) as a root node,
and another with 4 (height is 0).
We will end up having two different sets:
As you might notice, choosing the root of the node with the lowest height, has given us a skewed tree.
Implementation
Besides keeping a list of parents as we did in Quick Union, we also need a rank value for each node, which indicates its height. Then, we will use this value to pick our root node.
class UnionFind:
def __init__(self, n: int) -> None:
self.n = n
self.parents = [i for i in range(self.n)]
self.ranks = [1] * self.n
def union(self, a: int, b: int) -> None:
self._validate(a)
self._validate(b)
parent_a = self.find(a)
parent_b = self.find(b)
if parent_a == parent_b:
return
rank_a = self.ranks[a]
rank_b = self.ranks[b]
same_rank = rank_a == rank_b
if rank_a <= rank_b:
self.parents[parent_a] = parent_b
if same_rank:
self.ranks[b] += 1
else:
self.parents[parent_b] = parent_a
def find(self, a: int) -> int:
while a != self.parents[a]:
a = self.parents[a]
return a
def connected(self, a: int, b: int) -> bool:
return self.find(a) == self.find(b)
def _validate(self, a: int) -> None:
assert 0 <= a < self.n
If we apply this approach to the Find if Path Exists in Graph problem, finally our code will be accepted.
from typing import List
class Solution:
def validPath(
self, n: int, edges: List[List[int]], source: int, destination: int
) -> bool:
union_find = self.build_disjoint_set(n, edges)
return union_find.connected(source, destination)
def build_disjoint_set(self, n: int, edges: List[List[int]]) -> UnionFind:
union_find = UnionFind(n)
for a, b in edges:
union_find.union(a, b)
return union_find
Complexity
The space complexity is ,
since we have to store all parents and ranks in two lists of elements
(, hence ).
Regarding the time complexity,
the union function just depends on the find one.
This ranking approach ensures that the complexity is , where is the height of the set, which is always balanced thanks to this ranking properties. Hence, the final complexity will be .
Lastly, since we need to union edges, before finding out if two nodes are connected, we need time in total.
Path Compression
The Path Compression is an optimization technique,
which can be applied to the Quick Union implementation.
Let's suppose to have a skewed scenario like:
A find applied on node 3 would traverse all nodes.
Calling the function again would cause the same number of iterations.
However, what if we use the find function to group the nodes into the root one?
Basically, the example above would become the following after calling find(3).
The next find(3) will be must faster.
Implementation
As explained above,
only the find must be changed to accomplish such optimization:
class UnionFind:
def __init__(self, n: int) -> None:
self.n = n
self.parents = [i for i in range(self.n)]
def union(self, a: int, b: int) -> None:
self._validate(a)
self._validate(b)
parent_a = self.find(a)
parent_b = self.find(b)
if parent_a != parent_b:
self.parents[parent_b] = parent_a
def find(self, a: int) -> int:
if a == self.parents[a]:
return a
self.parents[a] = self.find(self.parents[a])
return self.parents[a]
def connected(self, a: int, b: int) -> bool:
return self.find(a) == self.find(b)
def _validate(self, a: int) -> None:
assert 0 <= a < self.n
If we apply such approach in the Find if Path Exists in Graph problem, finally our code will be accepted.
from typing import List
class Solution:
def validPath(
self, n: int, edges: List[List[int]], source: int, destination: int
) -> bool:
union_find = self.build_disjoint_set(n, edges)
return union_find.connected(source, destination)
def build_disjoint_set(self, n: int, edges: List[List[int]]) -> UnionFind:
union_find = UnionFind(n)
for a, b in edges:
union_find.union(a, b)
return union_find
Complexity
The space complexity is ,
since we have to store all parents in a list of elements.
Regarding the time complexity,
the union function just depends on the find one.
This kind of balancing allow us to achieve a similar time complexity compared to Quick Union Find by Rank, hence, .
Lastly, since we need to union edges, before finding out if two nodes are connected, we need time in total.
Union by Rank + Path Compression
These two optimizations can be combined to achieve a , where is the inverse Ackermann function, which can be considered on average.
Implementation
class UnionFind:
def __init__(self, n: int) -> None:
self.n = n
self.parents = [i for i in range(self.n)]
self.ranks = [1] * self.n
def union(self, a: int, b: int) -> None:
self._validate(a)
self._validate(b)
parent_a = self.find(a)
parent_b = self.find(b)
if parent_a == parent_b:
return
rank_a = self.ranks[a]
rank_b = self.ranks[b]
same_rank = rank_a == rank_b
if rank_a <= rank_b:
self.parents[parent_b] = parent_a
if same_rank:
self.ranks[b] += 1
else:
self.parents[parent_a] = parent_b
def find(self, a: int) -> int:
if a == self.parents[a]:
return a
self.parents[a] = self.find(self.parents[a])
return self.parents[a]
def connected(self, a: int, b: int) -> bool:
return self.find(a) == self.find(b)
def _validate(self, a: int) -> None:
assert 0 <= a < self.n
Again, applied to Find if Path Exists in Graph problem, our solution will be accepted.
from typing import List
class Solution:
def validPath(
self, n: int, edges: List[List[int]], source: int, destination: int
) -> bool:
union_find = self.build_disjoint_set(n, edges)
return union_find.connected(source, destination)
def build_disjoint_set(self, n: int, edges: List[List[int]]) -> UnionFind:
union_find = UnionFind(n)
for a, b in edges:
union_find.union(a, b)
return union_find
Topological Sorting
Topological Sorting is a linear ordering of Vertices in a Directed Acyclic Graph (also known as DAG),
such that for every directed edge , vertex appears before [1].
There might be more than one orders.
In fact, for the following graph:
We can have these three orders:
[a, b, c, d]
[a, c, b, d]
[a, c, d, b]
Usage
This sorting is widely used to schedule tasks, solve dependencies and plan course prerequisite.
The Kahn's algorithm can be used to implement such sorting.
It uses in-degrees of vertices. The vertices with zero in-degrees are repeatedly removed and the corresponding neighbors' in-degrees are updated accordingly.
Example
The Course Schedule is a classic problem where we can apply Topological Sorting by using the Kahn's algorithm.
References
Weighted Graphs
The type of edges of a Graph allows us to defined either Directed or Undirected graphs. However, the edges could also have weights, which represent the cost of moving between the vertices connected by these edges.
Shortest Path
We cannot use the standard BFS traversal to calculate the shortest path between two vertices. In fact, this implementation simply assumes the same cost for each edge, which is not true for weighted ones.
To overcome this problem, we could use some well-known algorithms.
For all of them, we are using the Network Delay Time problem to apply such algorithms.
Bellman–Ford algorithm
The Bellman–Ford algorithm can be applied to Graphs that have both positive and negative edges. However, it is slower compared to other ones. In fact, the algorithms runs in time.
from collections import deque
from typing import Dict, List, Tuple
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
graph = self.get_adjacency_list(times, n)
return self.bfs(graph, k)
def bfs(self, graph: Dict[int, List[Tuple[int, int]]], root: int) -> int:
queue = deque([root])
# the first node is `1`, not `0`
# hence, for simplicity, we create a list of `n + 1` values
distances = [float("inf")] * (len(graph) + 1)
distances[root] = 0
# we have to exclude it once we calculate the maximum below
distances[0] = float("-inf")
while queue:
node = queue.popleft()
for neighbor, weight in graph[node]:
new_distance = distances[node] + weight
if distances[neighbor] <= new_distance:
continue
queue.append(neighbor)
distances[neighbor] = new_distance
ans = max(distances)
return -1 if ans == float("inf") else ans
def get_adjacency_list(
self, times: List[List[int]], n: int
) -> Dict[int, List[Tuple[int, int]]]:
graph: Dict[int, List[Tuple[int, int]]] = {i: [] for i in range(1, n + 1)}
for a, b, weight in times:
graph[a].append((b, weight))
return graph
Dijkstra's algorithm
The Dijkstra's algorithm can be applied to Graphs that have only positive edges. However, it is faster compared to the Bellman–Ford algorithm. In fact, the algorithms runs in time.
import heapq
from typing import Dict, List, Tuple
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
graph = self.get_adjacency_list(times, n)
return self.bfs(graph, k)
def bfs(self, graph: Dict[int, List[Tuple[int, int]]], root: int) -> int:
queue = [(0, root)]
# the first node is `1`, not `0`
# hence, for simplicity, we create a list of `n + 1` values
distances = [float("inf")] * (len(graph) + 1)
distances[root] = 0
# we have to exclude it once we calculate the maximum below
distances[0] = float("-inf")
while queue:
_, node = heapq.heappop(queue)
for neighbor, weight in graph[node]:
new_distance = distances[node] + weight
if distances[neighbor] <= new_distance:
continue
heapq.heappush(queue, (new_distance, neighbor))
distances[neighbor] = new_distance
ans = max(distances)
return -1 if ans == float("inf") else ans
def get_adjacency_list(
self, times: List[List[int]], n: int
) -> Dict[int, List[Tuple[int, int]]]:
graph: Dict[int, List[Tuple[int, int]]] = {i: [] for i in range(1, n + 1)}
for a, b, weight in times:
graph[a].append((b, weight))
return graph
Intervals
Interval problems are often provided as a List as input,
where each element is either a List or a Tuple of two elements.
«-----»
a b
«--------»
c d
«--------»
e f
The most common operations we can perform on a list of intervals are:
- Checking if they overlap.
- Merging overlapping intervals.
Overlapping intervals
Let's take a simple interval (a, b) as an example:
«-----»
a b
For another interval (c, d) to overlap, the c point must be somewhere between a and b:
«-----»
a b
«---...
c
Which forms the first condition . However, this not sufficient for the overlapping. In fact, let's have a look at this example:
«-----»
a b
«-»
c d
So, also the d must be in a certain position compared to the other interval,
which is behind a:
«-----»
a b
«--------»
c d
Then, our overlapping condition is: 1.
Merging intervals
Again, let's draw some intervals to get the idea:
«-------»
a b
«--------»
c d
«-------»
a b
«--------»
c d
It looks way simpler now:
x, y = [
max(a, c),
min(b, d),
]
-
You can use this simple trick to memorize the formula. The symbol is always , so nothing special here. For the actual condition, just memorize that you start from
band then go tilla, thusbcandda. Yes, this is not rocket science. 🚀 ↩
Heaps
A Heap is a Tree-based data structure that satisfies the heap property [1]:
Min Heap: for any node , its parent is .Max Heap: for any node , its parent is .
The Heap is an extremely efficient implementation of the Priority Queue abstract data type.
In fact, priority queues are often simply called "heaps" regardless of their specific implementation [1].
A Priority Queue allows very similar operations compared to Queues,
but with the difference that we can also assign a priority to the items,
which could prioritize or de-prioritize the item based on its value.
Operations
Let's check the complexity of heaps' common operations:
| Operation | Time Complexity | Space Complexity | Syntax |
|---|---|---|---|
| Size | len(heap) | ||
| Heapify1 | heapq.heapify(lst) | ||
| Minimum | min_heap[0] | ||
| Maximum | max_heap[0] |
Usage
Check the heap section in the Python cheatsheet.
References
-
Heapify is the process of converting a
listinto aheap. ↩
Backtracking
Backtracking algorithms heavily use DFS1 to enumerate all the possible solutions to a problem.
These candidates are expressed as the nodes of a tree structure, which is the potential Search Tree [1].
Examples
The Subsets is a classic problem suitable for Backtracking.
At each call, we can decide whether or not to include the current element.
This decision requires two different function calls
that will derive the following Search Tree from the input [1, 2, 3].
If we collect the results of the 8 leaf nodes, we will get all our subsets.
Analyze the Complexity
The Time Complexity is proportional to the number of nodes in the Search Tree,
multiplied by the amount of work we do in each call.
We can use the formula to derive the number of nodes.
If we apply this formula to the previous problem,
we get and , where the height is actually the number of nodes in the input.
Plus, we need to consider the work we do to append the solutions to the final result list,
which is an additional time.
This would make the entire complexity to .
The Space Complexity is proportional to the height of the Search Tree.
In fact, once we reach a leaf node,
we simply terminate our search and go back to the parent nodes.
References
Dynamic Programming
Dynamic Programming problems can be solved by a Bottom-up approach and Top-down one.
In the former,
we solve the sub-problems first and then build up the solution.
In the latter,
we use a very similar approach compared to Backtracking:
we still build our Search Tree,
but we also avoid to re-calculate overlapping problems.
In order to do so, we can adopt a technique called Memoization,
which is a simple container of our solutions.
I personally prefer the Top-down one,
since it comes more naturally to implement once you have derived the Search Tree.
Example
A classic problem to apply Dynamic Programming is the Fibonacci one.
The naive solution would be something like:
def fib(n: int) -> int:
if n <= 1:
return n
return fib(n - 1) + fib(n - 2)
Which has a Time and Space complexity of and , respectively.
To understand how to apply Dynamic Programming,
let's derive the Search Tree of the previous snippet for fib(4).
As you can see,
there are two calls for fib,
but do we actually need both of them?
The answer is no, and we can use Memoization to store the result of fib(2).
A Dictionary suits very well to perform such task.
from typing import Dict
def fib(n: int) -> int:
def dfs(n: int, memo: Dict[int, int]) -> int:
assert n >= 0
if n <= 1:
return n
if n in memo:
return memo[n]
res = 0
res += dfs(n - 1, memo)
res += dfs(n - 2, memo)
memo[n] = res
return memo[n]
return dfs(n, {})
Thanks to this kind of cache,
we are able to avoid some function calls and this reduces the previous Space Tree to:
Which means that we also reduce our Time complexity to .
functools.lru_cache
The same result can be achieved by using the lru_cache decorator from functools.
from functools import lru_cache
@lru_cache
def fib(n: int) -> int:
if n <= 1:
return n
return fib(n - 1) + fib(n - 2)
Divide and Conquer
A Divide and Conquer algorithm recursively breaks down a problem into two or more sub-problems of the same or related type,
until these become simple enough to be solved.
The solutions to the sub-problems are then combined to give a solution to the original problem [1].
Merge Sort
The Merge Sort is a classic Divide and Conquer algorithm [2].
This algorithm can be divided into two steps [2]:
- Divide the input list into
nsub-lists, each containing one element. - Repeatedly
mergethese sub-lists to produce new sorted sub-lists. Thismergeprocess is repeated until there is only one sub-list remaining.
from typing import List
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
return self.merge_sort(nums)
def merge_sort(self, nums: List[int]) -> List[int]:
"""
Step 1) described above
"""
if len(nums) <= 1:
return nums
mid = len(nums) // 2
left = self.merge_sort(nums[:mid])
right = self.merge_sort(nums[mid:])
return self.merge(left, right)
def merge(self, a: List[int], b: List[int]) -> List[int]:
"""
Step 2) described above
"""
res = []
n, m = len(a), len(b)
i = j = 0
while i < n and j < m:
if a[i] < b[j]:
res.append(a[i])
i += 1
else:
res.append(b[j])
j += 1
# add remained elements from `a` (if any)
res.extend(a[i:])
# add remained elements from `b` (if any)
res.extend(b[j:])
return res
The solution can be verified here.
References
- [1]: https://en.wikipedia.org/wiki/Divide-and-conquer_algorithm
- [2]: https://en.wikipedia.org/wiki/Merge_sort
Python for Coding Interviews
This section summarizes all the Python constructs you need to solve any LeetCode problem.
I would be quite surprised if you need something else to do so.
All the information that you see here comes from a repository I created a few years back, which is python-for-coding-interviews.
Whatever you find here, it is also in the repository, where you can find a PDF.
Feel free to open PRs in the repository if you think that something is missing.
In any case, I will also include a Python section in every topic,
where I will explain the actual things you need to know and likely use.
🐍 Enjoy! 🐍
Table of contents
Primitive Types
- Booleans (
bool). - Integers (
int). - Floats (
float). - Strings (
str).
# Define variables
>>> b, i, f, s = True, 12, 8.31, 'Hello, world!'
>>> type(b) # <class 'bool'>
>>> type(i) # <class 'int'> ~ Unbounded
>>> type(f) # <class 'float'> ~ Bounded
>>> type(s) # <class 'str'>
# Type Conversion
>>> str(i)
'12'
>>> float(i)
12.0
>>> str(b)
'True'
>>> int('10')
10
>>> int('10a') # `ValueError: invalid literal for int() with base 10: '10a'`
# Operations
>>> 5 * 2
10
>>> 5 * 2.
10.0
>>> 5 / 2
2.5
>>> 5 // 2 # `//` is the integer division
2
>>> 5 % 2
1
# `min` and `max`
>>> min(4, 2)
2
>>> max(21, 29)
29
# Some useful math functions
>>> abs(-1.2)
1.2
>>> divmod(9, 4)
(2, 1)
>>> 2 ** 3 # Equivalent to `pow(2, 3)`
8
# Math functions from the `math` package
>>> import math
>>> math.ceil(7.2)
8
>>> math.floor(7.2)
7
>>> math.sqrt(4)
2.0
# Pseudo lower and upper bounds
>>> float('-inf') # Pseudo min-int
-inf
>>> float('inf') # Pseudo max-int
inf
# Pseudo lower and upper bounds (Python >= 3.5)
>>> import math
>>> math.inf
inf
>>> -math.inf
-inf
range and enumerate
# `range`
>>> list(range(3)) # Equivalent to `range(0, 3)`
[0, 1, 2]
>>> list(range(1, 10, 2))
[1, 3, 5, 7, 9]
>>> for i in range(3): print(i)
0
1
2
>>> for i in range(2, -1, -1): print(i) # Equivalent to `reversed(range(3))`
2
1
0
# `enumerate`
>>> for i, v in enumerate(range(3)): print(i, v)
0 0
1 1
2 2
>>> for i, v in enumerate(range(3), start=10): print(i, v)
10 0
11 1
12 2
# Reversed `enumerate`
>>> for i, v in reversed(list(enumerate(['a', 'b', 'c']))): print(i, v)
2 c
1 b
0 a
Tuples
>>> t = (1, 2, 'str')
>>> type(t)
<class 'tuple'>
>>> t
(1, 2, 'str')
>>> len(t)
3
>>> t[0] = 10 # Tuples are immutable: `TypeError: 'tuple' object does not support item assignment`
>>> a, b, c = t # Unpacking
>>> a
1
>>> b
2
>>> c
'str'
>>> a, _, _ = t # Unpacking: ignore second and third elements
>>> a
1
Lists
Python uses Timsort algorithm in sort and sorted (https://en.wikipedia.org/wiki/Timsort).
# Define a list
>>> l = [1, 2, 'a']
>>> type(l) # <class 'list'>
>>> len(l)
3
>>> l[0] # First element of the list
1
>>> l[-1] # Last element of the list (equivalent to `l[len(l) - 1]`)
'a'
# Slicing
>>> l[:] # `l[start:end]` which means `[start, end)`
[1, 2, 'a']
>>> l[0:len(l)] # `start` is 0 and `end` is `len(l)` if omitted
[1, 2, 'a']
# Some useful methods
>>> l.append('b') # `O(1)`
>>> l.pop() # `O(1)` just for the last element
'b'
>>> l.pop(0) # `O(n)` since list must be shifted
1
>>> l
[2, 'a']
>>> l.remove('a') # `O(n)`
>>> l.remove('b') # `ValueError: list.remove(x): x not in list`
>>> l
[2]
>>> l.index(2) # It returns first occurrence (`O(n)`)
0
>>> l.index(12) # `ValueError: 12 is not in list`
# More compact way to define a list
>>> l = [0] * 5
>>> l
[0, 0, 0, 0, 0]
>>> len(l)
5
>>> [k for k in range(5)]
[0, 1, 2, 3, 4]
>>> [k for k in reversed(range(5))]
[4, 3, 2, 1, 0]
# Compact way to define 2D arrays
>>> rows, cols = 2, 3
>>> m = [[0] * cols for _ in range(rows)]
>>> len(m) == rows
True
>>> all(len(m[k]) == cols for k in range(rows))
True
# Built-in methods
>>> l = [3, 1, 2, 0]
>>> len(l)
4
>>> min(l)
0
>>> max(l)
3
>>> sum(l)
6
>>> any(v == 3 for v in l)
True
>>> any(v == 5 for v in l)
False
>>> all(v >= 0 for v in l)
True
# Sort list in-place (`sort`)
>>> l = [10, 2, 0, 1]
>>> l
[10, 2, 0, 1]
>>> l.sort() # It changes the original list
>>> l
[0, 1, 2, 10]
>>> l.sort(reverse=True) # It changes the original list
>>> l
[10, 2, 1, 0]
# Sort a list a return a new one (`sorted`)
>>> l = [10, 2, 0, 1]
>>> sorted(l) # It returns a new list
[0, 1, 2, 10]
>>> l # Original list is not sorted
[10, 2, 0, 1]
# Sort by a different key
>>> students = [
('Mark', 21),
('Luke', 20),
('Anna', 18),
]
>>> sorted(students, key=lambda s: s[1]) # It returns a new list
[('Anna', 18), ('Luke', 20), ('Mark', 21)]
>>> students.sort(key=lambda s: s[1]) # In-place
>>> students
[('Anna', 18), ('Luke', 20), ('Mark', 21)]
Strings
>>> s = 'Hello, world!'
>>> type(s) # <class 'str'>
>>> len(s)
13
>>> s[0] = 'h' # Strings are immutable: `TypeError: 'str' object does not support item assignment`
>>> s += ' Another string' # A new string will be created, so concatenation is quite slow
>>> s = 'Hello'
>>> l = list(s)
>>> l
['H', 'e', 'l', 'l', 'o']
>>> l[0] = 'h'
>>> ''.join(l)
'hello'
>>> 'lo' in s
True
>>> ord('a')
97
>>> chr(97)
'a'
Stacks
>>> stack = [] # We can use a normal list to simulate a stack
>>> stack.append(0) # `O(1)`
>>> stack.append(1)
>>> stack.append(2)
>>> len(stack)
3
>>> stack[0] # Bottom of the stack
0
>>> stack[-1] # Top of the stack
2
>>> stack.pop() # `O(1)`
2
>>> stack.pop()
1
>>> len(stack)
1
>>> stack.pop()
0
>>> stack.pop() # `IndexError: pop from empty list`
>>> stack[-1] # `IndexError: pop from empty list`
Queues
>>> from collections import deque
>>> queue = deque()
# Enqueue -> append()
>>> queue.append(0) # `O(1)`
>>> queue.append(1)
>>> queue.append(2)
>>> len(queue)
3
>>> queue[0] # Head of the queue
0
>>> queue[-1] # Tail of the queue
2
# Dequeue -> popleft()
>>> queue.popleft() # `O(1)`
0
>>> queue.popleft()
1
>>> len(queue)
1
>>> queue.popleft()
2
>>> len(queue)
0
>>> queue.popleft() # `IndexError: pop from an empty deque`
>>> queue[0] # `IndexError: pop from an empty deque`
Sets
>>> s = set()
>>> s.add(1)
>>> s.add(2)
>>> s
{1, 2}
>>> len(s)
2
>>> s.add(1) # Duplicate elements are not allowed per definition
>>> s
{1, 2}
>>> s.add('a') # We can mix types
>>> s
{1, 2, 'a'}
>>> 1 in s # `O(1)`
True
>>> s.remove(1)
>>> s
{2, 'a'}
>>> s.remove(1) # `KeyError: 1`
>>> s.discard(1) # It won't raise `KeyError` even if the element does not exist
>>> s.pop() # Remove and return an arbitrary element from the set
2
>>> s0 = {1, 2, 'a'}
>>> s0
{1, 2, 'a'}
>>> s1 = set([1, 2, 'a'])
>>> s1
{1, 2, 'a'}
>>> s0 = {1, 2}
>>> s1 = {1, 3}
>>> s0 | s1
{1, 2, 3}
>>> s0.union(s1) # New set will be returned
{1, 2, 3}
>>> s0 = {1, 2}
>>> s1 = {1, 3}
>>> s0 & s1
{1}
>>> s0.intersection(s1) # New set will be returned
{1}
>>> s0 = {1, 2}
>>> s1 = {1, 3}
>>> s0 - s1
{2}
>>> s0.difference(s1)
{2}
Hash Tables
>>> d = {'a': 'hello, world', 'b': 11} # Equivalent to `dict(a='hello, world', b=11)`
>>> type(d)
<class 'dict'>
>>> d
{'a': 'hello, world', 'b': 11}
>>> d.keys()
dict_keys(['a', 'b'])
>>> d.values()
dict_values(['hello, world', 11])
>>> for k, v in d.items(): print(k, v)
a hello, world
b 11
>>> 'a' in d # `O(1)`
True
>>> 1 in d
False
>>> d['a'] += '!'
>>> d
{'a': 'hello, world!', 'b': 11}
>>> d[1] = 'a new element'
>>> d
{'a': 'hello, world!', 'b': 11, 1: 'a new element'}
>>> d[0] += 10 # `KeyError: 0`
>>> d.get(0, 1) # Return `1` as default value since key `0` does not exist
1
>>> d.get(1, '?') # Key `1` exists, so the actual value will be returned
'a new element'
>>> d.get(10) is None
True
Heaps
The following commands show how to work with a min heap.
Currently, Python does not have public methods for the max heap.
You can overcome this problem by applying one of the following strategies:
- Invert the value of each number. So, for example, if you want to add
1, 2 and 3 in the min heap, you can
heappush-3, -2 and -1. When youheappopyou invert the number again to get the proper value. This solution clearly works if your domain is composed by numbers >= 0. - Invert your object comparison.
>>> import heapq
>>> min_heap = [3, 2, 1]
>>> heapq.heapify(min_heap)
>>> min_heap
[1, 2, 3]
>>> min_heap = []
>>> heapq.heappush(min_heap, 3) # `O(log n)`
>>> heapq.heappush(min_heap, 2)
>>> heapq.heappush(min_heap, 1)
>>> min_heap
[1, 3, 2]
>>> len(min_heap)
>>> min_heap[0]
1
>>> heapq.heappop(min_heap) # `O(log n)`
1
>>> min_heap
[2, 3]
>>> heapq.heappop(min_heap)
2
>>> heapq.heappop(min_heap)
3
>>> heapq.heappop(min_heap) # `IndexError: index out of range`
collections
Container data types in the (collections package).
collections.namedtuple
>>> from collections import namedtuple
>>> Point = namedtuple('Point', 'x y')
>>> p0 = Point(1, 2)
>>> p0
Point(x=1, y=2)
>>> p0.x
1
>>> p0.y
2
>>> p1 = Point(x=1, y=2)
>>> p0 == p1
True
# Python >= 3.6.1
>>> from typing import NamedTuple
>>> class Point(NamedTuple):
x: int
y: int
>>> p0 = Point(1, 2)
>>> p1 = Point(x=1, y=2)
>>> p0 == p1
True
collections.defaultdict
>>> from collections import defaultdict
>>> d = defaultdict(int)
>>> d['x'] += 1
>>> d
defaultdict(<class 'int'>, {'x': 1})
>>> d['x'] += 2
>>> d
defaultdict(<class 'int'>, {'x': 3})
>>> d['y'] += 10
>>> d
defaultdict(<class 'int'>, {'x': 3, 'y': 10})
>>> d = defaultdict(list)
>>> d['x'].append(1)
>>> d['x'].append(2)
>>> d
defaultdict(<class 'list'>, {'x': [1, 2]})
collections.Counter
>>> from collections import Counter
>>> c = Counter('abcabcaa')
>>> c
Counter({'a': 4, 'b': 2, 'c': 2})
>>> c.keys()
dict_keys(['a', 'b', 'c'])
>>> c.items()
dict_items([('a', 4), ('b', 2), ('c', 2)])
>>> for k, v in c.items(): print(k, v)
a 4
b 2
c 2
>>> c['d'] # It acts as a `defaultdict` for missing keys
0
collections.OrderedDict
Please, notice that, since Python 3.6,
the order of items in a dictionary is guaranteed to be preserved.
>>> from collections import OrderedDict
>>> d = OrderedDict()
>>> d['first'] = 1
>>> d['second'] = 2
>>> d['third'] = 3
>>> d
OrderedDict([('first', 1), ('second', 2), ('third', 3)])
>>> for k, v in d.items(): print(k, v)
first 1
second 2
third 3
Grind 75
Grind 75 is an updated list of problems
from the author of Blind 75.
This list actually contains a total of 169 questions.
However, I will start from the first 75 and then add the other ones gradually.
Lastly, I have just replaced String to Integer (atoi) with Two Sum II - Input Array Is Sorted, which is much more useful.
Approach a Problem
The Tech Interview Handbook provides a great list of steps that could be used to approach and solve coding interview questions.
Be sure to familiarize with such steps and try to apply them also when you solve LeetCode questions by yourself.
Two Sum
The problem description can be found in LeetCode.
Approach
A brute force approach would consist of generating all possible pairs in the input list and calculate the sum. This would require time and space. The code would look something like this:
from typing import List
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
n = len(nums)
for i in range(n):
for j in range(i + 1, n):
curr_sum = nums[i] + nums[j]
if curr_sum == target:
return [i, j]
raise Exception("expected one solution")
Of course, we can do better in term of time. For sure, we have to iterate until the end of the list, but then we need an auxiliary data structure to use to memorize something.
We could store the complement of the i-th number
and then look for it the next iteration.
If the i-th number is already in our collection,
then it means that we found the other addend.
For a quick look-up table, we can use a Python dictionary.
Let's take an example:
nums = [1, 2, 10]
target = 3
Initially, our dictionary will be empty.
The first number to check is 1,
which means that our complement is 2 (target - current num).
So our dictionary will be the following after the first iteration:
d = {
2: 0,
}
Where the key is the complement, and the value is the index
(remember that we have to return the index of the two numbers).
Then, in the second iteration,
we can see that number 2 is already in the dictionary,
which means that we found the second addend.
Hence, we can return the index in the dictionary entry and the current one.
Solution
from typing import Dict, List
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
comps: Dict[int, int] = {}
for i, num in enumerate(nums):
if num in comps:
return [comps[num], i]
comp = target - num
comps[comp] = i
raise Exception("expected one solution")
Complexity
- Time:
- Space:
Where is the size of the list nums.
Best Time to Buy and Sell Stock
The problem description can be found in LeetCode.
Approach
As usual, we could apply a brute force approach.
We could start from the first price and consider it as a buy price and
then look for a higher price in the range [1, n - 1] to make a profit
(n is the size of the prices list).
Then, we could start from the second price and loop for values in the range [2, n - 1].
We could go on until the end of the prices list and store the maximum profit we can obtain.
This approach would require time because of this double looping.
However, this is not really necessary. In fact, let's look at this example:
prices = [1, 2, 3, 4, 5, 6]
For an ordered list,
the maximum profit we can achieve is between the minimum and the maximum values.
So, for an increasing sequence, we need to consider the first value,
which is the minimum of the sequence itself,
as our buy price.
Now, let's look at the example of the question description:
prices = [7, 1, 5, 3, 6, 4]
We can easily understand that it makes no sense to consider the 7,
since we will surely get a higher profit with its next element 1.
In fact, if there is a higher price later in the list,
we would get the best profit with 1 and not with 7.
So, we could point a first index to the minimum element we encountered so far and increment the second pointer by one at each iteration. Meanwhile, we also calculate the best profit so far by using these two pointers.
Solution
from typing import List
class Solution:
def maxProfit(self, prices: List[int]) -> int:
ans = 0
buy_price = prices[0] if len(prices) > 0 else 0
for price in prices[1:]:
if buy_price > price:
buy_price = price
else:
ans = max(ans, price - buy_price)
return ans
Complexity
- Time:
- Space:
Where is the size of the prices list.
Valid Palindrome
The problem description can be found in LeetCode.
Approach
A string is a palindrome if s == reversed(s),
so, for example, Anna is a palindrome, if we do a case insensitive comparison.
In contrast with the usual palindrome problem,
this question asks us to only compare alphanumeric characters ([a-zA-Z0-9]).
This is a classic example of a Two Pointers algorithm.
We can start one pointer at the beginning (left one) and
one on the end (right one).
If the two characters are alphanumeric,
we can compare them, otherwise,
we move the pointers until there are two alphanumeric characters to compare.
In general, we can then interrupt our algorithm if the characters are different, otherwise move both pointers. We will continue until the two pointers meet.
Solution
class Solution:
def isPalindrome(self, s: str) -> bool:
left, right = 0, len(s) - 1
while left < right:
if not self.is_alphanumeric(s[left]):
left += 1
elif not self.is_alphanumeric(s[right]):
right -= 1
else:
if s[left].lower() != s[right].lower():
return False
left += 1
right -= 1
return True
def is_alphanumeric(self, char: str) -> bool:
assert isinstance(char, str)
assert len(char) == 1
return "a" <= char <= "z" or "A" <= char <= "Z" or "0" <= char <= "9"
Note that the Python standard library offers the str.isalnum, which checks if all characters in the string are alphanumeric. So, we can rewrite the previous solution as:
class Solution:
def isPalindrome(self, s: str) -> bool:
left, right = 0, len(s) - 1
while left < right:
if not s[left].isalnum():
left += 1
elif not s[right].isalnum():
right -= 1
else:
if s[left].lower() != s[right].lower():
return False
left += 1
right -= 1
return True
Complexity
- Time:
- Space:
Where is the length of the string s.
Valid Anagram
The problem description can be found in LeetCode.
Approach
From the constraints we can see that both input strings (s and t) consist of lowercase English letters.
The first assumption we can make is that if the length of the two strings is different,
t will not be an anagram of s.
Since we know that the length of the two strings must be the same,
if we order all the characters of the two strings and the strings are equal,
it means that t is an anagram of s.
However, this would require , hence ,
for sorting both strings and then comparing them,
where is the length of the two strings.
Of course, we can do better in terms of time.
In fact, we could simply count the characters of both strings and
then compare the two counters to confirm that t is an anagram of s.
For example, for the strings "asd" a "sad", we would have:
s = "asd"
t = "sad"
counter_s = {
"a": 1,
"s": 1,
"d": 1,
}
counter_t = {
"s": 1,
"a": 1,
"d": 1,
}
assert(counter_s == counter_t)
The counters are the same, hence, we can return True.
Solution
Since our alphabet is limited to lowercase English characters,
we can use a static list of 26 elements,
instead of a dictionary.
The letter a is mapped to index 0 and z to 25.
Solution
from typing import List
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
if len(s) != len(t):
return False
return self.get_chars_counter(s) == self.get_chars_counter(t)
def get_chars_counter(self, s: str) -> List[int]:
m = [0] * 26
for char in s:
idx = ord(char) - ord("a")
m[idx] += 1
return m
We could also use a normal dictionary:
from collections import defaultdict
from typing import DefaultDict
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
if len(s) != len(t):
return False
return self.get_chars_counter(s) == self.get_chars_counter(t)
def get_chars_counter(self, s: str) -> DefaultDict[int, int]:
counter: DefaultDict[int, int] = defaultdict(int)
for char in s:
idx = ord(char) - ord("a")
counter[idx] += 1
return counter
As well as the built-in Counter:
from collections import Counter
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
if len(s) != len(t):
return False
return self.get_chars_counter(s) == self.get_chars_counter(t)
def get_chars_counter(self, s: str) -> Counter:
return Counter(s)
Complexity
- Time:
- Space:
Where is the length of the strings s and t.
Binary Search
We have already covered this problem in the Binary Search section.
First Bad Version
The problem description can be found in LeetCode.
Approach
The problem looks very easy.
It would be enough to iterate over the list and simply find the first bad version.
which means that you have to return the index of the first element that is True.
This simple solution would require time and space.
Sometimes it is very useful to draw pictures or write examples of the inputs to graphically represent the problem. This is a classic example where this could help a lot.
Let's write some examples:
versions1 = [False, True, True, True]
versions2 = [True, True, True, True]
versions3 = [False, False, False]
Which could be written as:
versions1 = [0, 1, 1, 1]
versions2 = [1, 1, 1, 1]
versions3 = [0, 0, 0]
Where False values are 0s and True values are 1s.
What do we notice?
Well, the input is already sorted. As usual, having a sorted list always means that Binary Search might be used.
In this particular case,
we can apply Binary Search to find the leftmost True value,
as we explained in the Binary Search ~ Additional Usage section.
Solution
class Solution:
def firstBadVersion(self, n: int) -> int:
left, right = 1, n
ans = -1
while left <= right:
mid = (left + right) // 2
if isBadVersion(mid):
ans = mid
right = mid - 1
else:
left = mid + 1
assert ans != -1, "expected one solution"
return ans
Complexity
- Time:
- Space:
Where is the number of versions, which the unique parameter of our function.
Ransom Note
The problem description can be found in LeetCode.
Approach
Usually, for problems that involve strings, we might need to use a counter dictionary for the characters.
In order to build our ransom note we need a certain number of characters, and all of them must be in the magazine. So we have to count such characters and check if we have enough of them in the magazine.
Since our alphabet is limited to lowercase English letters,
we can count them by using a static list of 26 elements
as we did for the Valid Anagram problem.
Once we have the two counters,
we can simply iterate over the one of the ransom note and
check if the magazine counter has enough occurrences for the i-th character:
from typing import List
class Solution:
def canConstruct(self, ransomNote: str, magazine: str) -> bool:
if len(ransomNote) > len(magazine):
return False
rn_counter = self.get_chars_counter(ransomNote)
m_counter = self.get_chars_counter(magazine)
for i, occ in enumerate(rn_counter):
if m_counter[i] < occ:
return False
return True
def get_chars_counter(self, s: str) -> List[int]:
m = [0] * 26
for char in s:
idx = ord(char) - ord("a")
m[idx] += 1
return m
This would take time and space,
where is the length of the magazine string
(which is greater than the size of the string ransomNote).
Even if this solution is accepted, there is a slightly better way to solve the issue.
In fact, for this kind of problems,
sometimes we can build a single counter and then apply some logic to it to verify its properties.
In this case, once we get the counter,
we can simply iterate over the ransomNote string and subtract the i-th character to the counter.
If the number of its occurrence is less than 0, it means that we do not have enough characters from the magazine,
hence, we cannot build the ransom note.
Please, notice that in terms of notation, the complexity is the same compared to the previous approach. However, the code will be faster since we are going to run less instructions.
Solution
from typing import List
class Solution:
def canConstruct(self, ransomNote: str, magazine: str) -> bool:
if len(ransomNote) > len(magazine):
return False
counter = self.get_chars_counter(magazine)
for char in ransomNote:
idx = self.get_idx_from_char(char)
counter[idx] -= 1
if counter[idx] < 0:
return False
return True
def get_chars_counter(self, s: str) -> List[int]:
m = [0] * 26
for char in s:
idx = self.get_idx_from_char(char)
m[idx] += 1
return m
def get_idx_from_char(self, char: str) -> int:
assert isinstance(char, str)
assert len(char) == 1
return ord(char) - ord("a")
Complexity
- Time:
- Space:
Where is the length of the magazine string.
Longest Palindrome
The problem description can be found in LeetCode.
Approach
The problem looks confusing at first, but it is actually very straight-forward.
Let's look at some examples in terms of input and output:
"aabb" -> 4
"aabbcc" -> 6
"abc" -> 1
"aabbc" -> 5
"aaabbbccc" -> 7
One thing we can notice here is that if a character has an even number of occurrences, we can simply consider all of them in our solution.
However, if we have an odd number of occurrences we need to be careful about what we have to take for our solution.
Let's take aaabbbccc as an example.
A possible solution could be aabbcc., where . can be any character from {a, b, c}.
This suggests that we can take |odd occurrences for a certain char| - 1 for our solution,
since it gives us as an even number.
Moreover, we have to take into account that we can have an extra character coming from such odd number of occurrences (as this example).
Solution
from typing import List
class Solution:
def longestPalindrome(self, s: str) -> int:
counter = self.get_chars_counter(s)
ans = 0
for i, rep in enumerate(counter):
if rep % 2 == 0:
ans += rep
counter[i] = 0
else:
ans += rep - 1
counter[i] = 1
if any(counter) == 1:
ans += 1
return ans
def get_chars_counter(self, s: str) -> List[int]:
# a b ... z A B ... Z
# 0 1 25 26 27 51
m = [0] * 52
for char in s:
if char.islower():
idx = ord(char) - ord("a")
elif char.isupper():
idx = ord(char) - ord("A") + 26
else:
raise Exception(
"expected either lower-case or upper-case character, "
f"but got `{char}`"
)
m[idx] += 1
return m
Complexity
- Time:
- Space:
Where is the size of the s string.
Majority Element
The problem description can be found in LeetCode.
Approach
For the optimal solution in terms of space and time, you can check the Boyer–Moore majority vote algorithm. Here, we are going to check a slightly simpler solution, which requires more space compared to the algorithm cited above.
As usual, let's derive some examples. As per the requirements, we are sure to have a majority element, so we cannot have lists like:
wrong_lst1 = [1, 2] # counter = {1: 1, 2: 1}, len(lst1) = 2
wrong_lst2 = [1, 2, 3] # counter = {1: 1, 2: 1, 3: 1}, len(lst1) = 3
In fact, in these cases the number of occurrences of a certain number is always the same.
So, let's use some valid ones:
lst1 = [1] # counter = {1: 1}, len(lst1) = 1
lst2 = [1, 1, 2] # counter = {1: 2, 2: 1}, len(lst2) = 3
lst3 = [1, 1, 1, 2, 2] # counter = {1: 3, 2: 2}, len(lst3) = 5
It is clear that the majority element has the highest number of repetitions. In particular, the number of occurrences is always , where is the size of the input list.
Hence, it will be enough to count the number of elements and then return the number that has a number of occurrences .
Solution
from collections import defaultdict
from typing import DefaultDict, List
class Solution:
def majorityElement(self, nums: List[int]) -> int:
counter = self.get_nums_counter(nums)
for num, occ in counter.items():
if occ > len(nums) // 2:
return num
raise Exception("expected one solution")
def get_nums_counter(self, nums: List[int]) -> DefaultDict[int, int]:
counter: DefaultDict[int, int] = defaultdict(int)
for num in nums:
counter[num] += 1
return counter
Complexity
- Time:
- Space:
Where is the size of the nums list.
Add Binary
The problem description can be found in LeetCode.
Approach
The problem is quite simple. We just need to start from the end of the string to start calculating the first digit of the sum and then go backward to calculate all the other digits.
So, the difficult part of the problem is to avoid the index out of range exception.
Solution
class Solution:
def addBinary(self, a: str, b: str) -> str:
i, j = len(a) - 1, len(b) - 1
ans = []
carry = 0
while i >= 0 or j >= 0:
num1 = int(a[i]) if i >= 0 else 0
num2 = int(b[j]) if j >= 0 else 0
s = num1 + num2 + carry
carry = s // 2
ans.append(str(s % 2))
i -= 1
j -= 1
if carry:
ans.append("1")
return "".join(reversed(ans))
Complexity
- Time:
- Space:
Where and are the size of the strings and , respectively.
Contains Duplicate
The problem description can be found in LeetCode.
Approach
A naive approach would consist of checking all possible pairs, which would require time.
Another possibility would consist of sorting the input array and then make a linear search to look at two consecutive elements to find out if a duplicate is present. This would require time for sorting and for the linear search, hence the total time complexity would be .
As usual, we can improve the overall time complexity by using an auxiliary data structures to keep track of some intermediate results. In this case, we can use a Set for a quick lookup of duplicated elements.
Solution
from typing import List
class Solution:
def containsDuplicate(self, nums: List[int]) -> bool:
seen = set()
for num in nums:
if num in seen:
return True
seen.add(num)
return False
The same algorithm can be implemented in a single line. However, this would create a set every time. So for inputs that contain duplicates at the very beginning, this algorithm would be slower compared to the first one, but the space and time complexity would remain the same.
from typing import List
class Solution:
def containsDuplicate(self, nums: List[int]) -> bool:
return len(set(nums)) != len(nums)
Complexity
- Time:
- Space:
Where is the size of the nums list.
Insert Interval
The problem description can be found in LeetCode.
Approach
This is a classic Interval problem.
We can divide the algorithm in three steps:
- Add the non-overlapping intervals smaller than the new one.
- Merge the overlapping intervals.
- Add the remaining intervals.
Solution
from typing import List
class Solution:
def insert(
self, intervals: List[List[int]], newInterval: List[int]
) -> List[List[int]]:
ans = []
i = 0
# 1.
while i < len(intervals) and intervals[i][1] < newInterval[0]:
ans.append(intervals[i])
i += 1
# 2.
while i < len(intervals) and intervals[i][0] <= newInterval[1]:
newInterval[0] = min(newInterval[0], intervals[i][0])
newInterval[1] = max(newInterval[1], intervals[i][1])
i += 1
ans.append(newInterval)
# 3.
while i < len(intervals):
ans.append(intervals[i])
i += 1
return ans
Complexity
- Time:
- Space:
Where is the size of the intervals list.
Longest Substring Without Repeating Characters
The problem description can be found in LeetCode.
Approach
This is a classic example of a Sliding Window with a Dynamic Size problem.
In fact, we can think of having an imaginary dynamic window of the string (a sub-string), which cannot contain duplicates. We can use a Set to keep track of such duplicates in constant time and we can shrink our window in case we found one. Then, after removing it, we can keep increasing our window to obtain the result.
Solution
from typing import Set
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
chars: Set[str] = set()
ans = left = 0
for right, char in enumerate(s):
while char in chars:
chars.remove(s[left])
left += 1
chars.add(char)
win_size = right - left + 1
ans = max(ans, win_size)
return ans
Complexity
- Time:
- Space:
Where is the size of the s string.
Regarding the space, since our alphabet is limited to English letters, digits, symbols and spaces,
it can be considered as constant.
In fact, the size of the chars set that we use to keep track of the repeated characters in the string does not depend
on the size of the input string.
Two Sum II - Input Array Is Sorted
Check the Two Pointers algorithm section.
3Sum
The problem description can be found in LeetCode.
Approach
Before solving this problem be sure to understand:
The most efficient way to solve this problem is to sort the input array,
and then use this property to efficiently look for the triplets that add up to 0.
In fact, we can "lock" the first element and then look for the other two in the remaining ordered list. In this way, since we are looking for:
By locking the first element, we can reduce our problem to:
So, we can apply a Two Sum II in the ordered list in order to get two numbers ( and )
that add up to .
We can repeat this process until we have numbers in the list.
Lastly, we need to be careful about the edge case, which consists of not locking the same element more than once to avoid to have duplicate solutions. For example, with:
nums = [-1, -1, 0, 0, 1]
We can lock the first -1 (index 0) and obtain a solution with 0 and 1.
However, we have to skip the next -1 (index 1) to avoid to include the same solution in the result again.
Solution
from typing import List
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums.sort()
prev = None
ans: List[List[int]] = []
for i, num in enumerate(nums):
# skip already seen element
if num == prev:
continue
# if current element `a` is > 0,
# it means that the next two `b` and `c` are > 0 since the list is sorted
#
# hence, there won't be any triplet which can add up to 0
if num > 0:
break
prev = num
# a + b + c = 0
# b + c = -a
#
# hence, look for -a
ans.extend([num, j, k] for j, k in self.two_sum(nums, -num, i + 1))
return ans
def two_sum(self, nums: List[int], target: int, left: int) -> List[List[int]]:
right = len(nums) - 1
ans = []
while left < right:
psum = nums[left] + nums[right]
if psum == target:
ans.append([nums[left], nums[right]])
left += 1
right -= 1
# move one of the two pointers to avoid duplicated pairs
while left < len(nums) and nums[left - 1] == nums[left]:
left += 1
elif psum < target:
left += 1
else:
right -= 1
return ans
Complexity
- Time:
- Space:
Where is the size of the nums list.
Product of Array Except Self
The problem description can be found in LeetCode.
Approach
This is a classic problem where we need to pre-calculate something that we are going to use later to build up the solution.
For example, with the following input:
nums = [1, 2, 3, 4]
# a b c d
We have to obtain:
ans = [24, 12, 8, 6]
Which is:
products = [b * c * d, a * c * d, a * b * d, a * b * c]
So, we need to calculate the result based on the operations listed above. One way to obtain them is to derive such products in two ways:
- From
lefttoright. - From
righttoleft.
In this way, we would get something like:
pre = [ 1, a, a * b, a * b * c]
post = [b * c * d, c * d, d, 1]
If we multiply the pre and post elements at the same index,
we would obtain the same operations compared to products,
which is our solution.
This solution would require for both time and space.
from typing import List
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
pre = [1] * len(nums)
post = [1] * len(nums)
# left to right
for i in range(1, len(nums)):
pre[i] = nums[i - 1] * pre[i - 1]
# right to left
for i in range(len(nums) - 2, -1, -1):
post[i] = nums[i + 1] * post[i + 1]
return [pre_v * post_v for pre_v, post_v in zip(pre, post)]
However,
we can avoid to keep track of the pre and post values,
but we can instead build such values directly in the list that stores the solution.
Solution
from typing import List
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
ans = [1 for _ in range(len(nums))]
# left to right
pre = 1
for i in range(1, len(nums)):
pre *= nums[i - 1]
ans[i] *= pre
# right to left
post = 1
for i in range(len(nums) - 2, -1, -1):
post *= nums[i + 1]
ans[i] *= post
return ans
Complexity
- Time:
- Space:
Where is the size of the nums list.
Merge Intervals
The problem description can be found in LeetCode.
Approach
This is a classic Interval problem.
Before merging the intervals, we need to sort them to avoid to check all possible pairs, which would require time.
Once sorted, we can iterate over the intervals and either add them to the result list or merge overlapping ones.
intervals = [
[0, 1],
[2, 3],
[4, 5],
]
Here, there is no interval overlap, so we can simply add all of them in the result list.
intervals = [
[0, 1],
[2, 3],
[2, 5],
[2, 15],
]
Here, the first two do not overlap.
So, we could add both of them in the result list.
However, the third one overlaps with.
How could we merge them?
Well, the lower bound cannot be smaller then 2,
since the intervals are sorted.
This means that the first value is always the same.
Regarding the second one, we need to be careful about an edge case, which would consist of something like:
intervals = [
[0, 10],
[5, 8],
]
The second value would be picked from the first interval and not from the second one. In fact, the intervals are sorted only by the first value, so we cannot make assumptions about the second one. For it, we have to consider the maximum between the one in the result list and the current interval.
Solution
from typing import List
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
intervals.sort()
ans: List[List[int]] = []
for interval in intervals:
if not ans or not self.overlap(interval, ans[-1]):
ans.append(interval)
else:
ans[-1][1] = max(ans[-1][1], interval[1])
return ans
def overlap(self, interval_0, interval_1):
a, b = interval_0
c, d = interval_1
return b >= c and d >= a
Complexity
- Time:
- Space:
Where is the size of the intervals list.
Time Based Key-Value Store
The problem description can be found in LeetCode.
Approach
As usual, asking clarifying questions is fundamental in a coding interview. For this problem in particular, we have the requirements stating that:
All the timestamps
timestampof set are strictly increasing.
This is so important in the design of the solution of this problem. In fact, this requirement is telling us that timestamp will be a sorted sequence in the end. Therefore, as we already read about in other problems, this is a clear indicator that Binary Search could be used to improve the overall time complexity.
Solution
from collections import defaultdict
class TimeMap:
def __init__(self):
self.d = defaultdict(list)
def set(self, key: str, value: str, timestamp: int) -> None:
self.d[key].append((value, timestamp))
def get(self, key: str, timestamp: int) -> str:
if key not in self.d:
return ""
vals = self.d[key]
left, right = 0, len(vals) - 1
idx = -1
while left <= right:
mid = (left + right) // 2
if vals[mid][1] <= timestamp:
left = mid + 1
idx = mid
else:
right = mid - 1
return vals[idx][0] if idx != -1 else ""
Complexity
set:- Time:
- Space:
get:- Time:
- Space:
Where is the size of the list pointed by the key key.
Sort Colors
The problem description can be found in LeetCode.
Approach
A naive approach would consist of counting the three numbers in a static array of length 3.
nums = [2, 0, 2, 1, 1]
Would be:
counter = [1, 2, 2]
| | |
0 1 2
Where counter maps the number of occurrences of the numbers 0, 1 and 2.
Then, we could rearrange the elements based on this counter array.
This is like using Counting sort.
from typing import List
class Solution:
def sortColors(self, nums: List[int]) -> None:
counter = [0, 0, 0]
for num in nums:
counter[num] += 1
for i in range(len(nums)):
if counter[0] > 0:
counter[0] -= 1
nums[i] = 0
elif counter[1] > 0:
counter[1] -= 1
nums[i] = 1
elif counter[2] > 0:
counter[2] -= 1
nums[i] = 2
Alternatively, we could think this problem as the Dutch national flag one.
Solution
from typing import List
class Solution:
def sortColors(self, nums: List[int]) -> None:
i = j = 0
k = len(nums) - 1
mid = 1
while j <= k:
if nums[j] < mid:
nums[i], nums[j] = nums[j], nums[i]
i += 1
j += 1
elif nums[j] > mid:
nums[j], nums[k] = nums[k], nums[j]
k -= 1
else:
j += 1
Complexity
- Time:
- Space:
Where is the size of the nums list.
Container With Most Water
The problem description can be found in LeetCode.
Approach
As usual, checking all possible pairs would require time. However, we can still use the Two Pointers algorithm to reduce it to .
Let's derive some examples:
|
| |
| | |
| | | |
| | | | | |
1 3 4 2 5 1
The first value is bounded to its height. We cannot use a higher height to maximize the height itself, since only the minimum between the two will be used. So, for this first value, the maximum area we can obtain is with the last value.
At this point, we can avoid to consider the same height area again, since we cannot obtain a higher area with it. This means that we can discard this height from the search and go to the next one.
Solution
from typing import List
class Solution:
def maxArea(self, heights: List[int]) -> int:
ans = 0
left, right = 0, len(heights) - 1
while left < right:
area = min(heights[left], heights[right]) * (right - left)
ans = max(ans, area)
if heights[left] < heights[right]:
left += 1
else:
right -= 1
return ans
Complexity
- Time:
- Space:
Where is the size of the heights1 list.
-
In LeetCode,
heightis used as parameter name. However, for lists, a plural variable name should be used. ↩
Spiral Matrix
The problem description can be found in LeetCode.
Approach
For this problem, it is enough to follow this pattern for the directions:
- Right.
- Down.
- Left.
- Up.
Then, we can repeat the process until the are elements to check.
We just need to be careful and avoid to visit an element more than once. We could use a Set to achieve this.
from enum import Enum
from typing import List, Tuple
class Direction(Enum):
UP = 0
DOWN = 1
LEFT = 2
RIGHT = 3
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
rows, cols = len(matrix), len(matrix[0])
n = rows * cols
pos = Direction.RIGHT
row = col = 0
ans: List[int] = []
visited = {(0, 0)}
stack = [(0, 0)]
while len(ans) != n:
row, col = stack.pop()
ans.append(matrix[row][col])
new_row, new_col = self.get_next_position(row, col, pos)
if (
not self.is_valid_position(new_row, new_col, rows, cols)
or (new_row, new_col) in visited
):
pos = self.change_position(pos)
new_row, new_col = self.get_next_position(row, col, pos)
stack.append((new_row, new_col))
visited.add((new_row, new_col))
return ans
def change_position(self, pos: Direction) -> Direction:
if pos == Direction.UP:
return Direction.RIGHT
if pos == Direction.DOWN:
return Direction.LEFT
if pos == Direction.LEFT:
return Direction.UP
if pos == Direction.RIGHT:
return Direction.DOWN
assert False, f"unknown position `{pos}`"
def get_next_position(self, row: int, col: int, pos: Direction) -> Tuple[int, int]:
if pos == Direction.UP:
return row - 1, col
if pos == Direction.DOWN:
return row + 1, col
if pos == Direction.LEFT:
return row, col - 1
if pos == Direction.RIGHT:
return row, col + 1
assert False, f"unknown position `{pos}`"
def is_valid_position(self, row: int, col: int, rows: int, cols: int) -> bool:
return 0 <= row < rows and 0 <= col < cols
This solution would work, but it requires extra space for both the next element to pick and the visited coordinates.
However, there is a better approach that won't use any extra space. Let's derive some examples:
a b c d
e f g h
i j k l
This would would require:
|cols|steps right.|rows| - 1steps down.|cols| - 1steps left.|rows| - 2steps up.|cols| - 2steps right.
Moreover, we can notice that between (right, down) and (left, up) only the directions are different. So, if we group these four operations into two groups, we would end up by just having horizontal (left and right) and vertical (up and down) movements.
Solution
from typing import List
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
rows, cols = len(matrix), len(matrix[0])
n = rows * cols
row, col = 0, -1
direction = 1
ans: List[int] = []
while len(ans) != n:
# horizontal
for _ in range(cols):
col += direction
ans.append(matrix[row][col])
rows -= 1
# vertical
for _ in range(rows):
row += direction
ans.append(matrix[row][col])
cols -= 1
direction *= -1
return ans
Complexity
- Time:
- Space:
Where and are the number for rows and columns of the matrix, respectively.
Search in Rotated Sorted Array
The problem description can be found in LeetCode.
Approach
Whenever we have a sorted sequence, there is a pretty high chance that Binary Search must be used.
Of course, there are variations of Binary Search. Here, the array is sorted, but rotated, which means that there are two distinct sorted lists.
Let's take at an example:
lst = [6, 7, 1, 2, 3, 4, 5]
<-->
<------------>
L M R
We can obtain two arrays by splitting the input one:
[L, M) and (M, R],
where L, M and R are left, mid and right, respectively.
We can also notice that (M, R] is the sorted array.
In fact, for each middle element, either the left array or the right one are actually sorted.
Since only one of them is actually sorted,
we can use this information to change either the left or the right pointer,
depending on the values of the mid element and the target one.
Solution
from typing import List
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
num_left = nums[left]
num_mid = nums[mid]
num_right = nums[right]
is_left_ordered = num_left <= num_mid
is_right_ordered = num_mid <= num_left
assert is_left_ordered or is_right_ordered
if is_left_ordered:
if num_left <= target <= num_mid:
right = mid - 1
else:
left = mid + 1
elif is_right_ordered:
if num_mid <= target <= num_right:
left = mid + 1
else:
right = mid - 1
return -1
Complexity
- Time:
- Space:
Where is the size of the nums list.
Longest Palindromic Substring
The problem description can be found in LeetCode.
Approach
If we think of a way to solve the problem without knowing much about programming, the first method we would probably try is to expand a possible palindrome string from any character (the centre of the string).
For example:
s = "aaa"
c -> center of the string
We could consider the second a as center and
expand the string on both left and right.
In this way, we would get the maximum palindrome,
which is the string itself.
The example above considers a string with an odd number of characters. What about a string with an even length?
s = "aaaa"
cc -> centers of the string
In this case, we would have two centers. So, it will be enough to start the pointers at two different positions.
Solution
from typing import Tuple
class Solution:
def longestPalindrome(self, s: str) -> str:
max_size = 0
left = right = 0
for i in range(len(s)):
o_left, o_right, o_size = self.get_palindrome(s, i, i)
if o_size > max_size:
left, right = o_left, o_right
max_size = o_size
e_left, e_right, e_size = self.get_palindrome(s, i, i + 1)
if e_size > max_size:
left, right = e_left, e_right
max_size = e_size
return s[left : right + 1]
def get_palindrome(self, s: str, left: int, right: int) -> Tuple[int, int, int]:
while left >= 0 and right < len(s) and s[left] == s[right]:
left -= 1
right += 1
return left + 1, right - 1, right - left + 1
Complexity
- Time:
- Space:
Where is the size of the s string.
Find All Anagrams in a String
The problem description can be found in LeetCode.
Approach
This is a classic Sliding Window with a Static Size problem.
In fact, all we need to do is to keep track of a static window of size |p| by checking the characters of the string s.
Once the window with such size is completed,
we can compare it with the counter of the string p.
If they are equal, it means that we found a valid anagram.
Solution
from typing import List
class Solution:
def findAnagrams(self, s: str, p: str) -> List[int]:
if len(p) > len(s):
return []
s_counter = self.get_default_counter()
p_counter = self.get_chars_counter(p)
ans = []
left = 0
for right, char in enumerate(s):
s_counter[self.get_counter_idx(char)] += 1
win_size = right - left + 1
if win_size > len(p):
s_counter[self.get_counter_idx(s[left])] -= 1
left += 1
if p_counter == s_counter:
ans.append(left)
return ans
def get_default_counter(self) -> List[int]:
return [0] * 26
def get_counter_idx(self, char: str) -> int:
assert isinstance(char, str)
assert len(char) == 1
assert "a" <= char <= "z"
return ord(char) - ord("a")
def get_chars_counter(self, s: str) -> List[int]:
counter = self.get_default_counter()
for char in s:
counter[self.get_counter_idx(char)] += 1
return counter
Complexity
- Time:
- Space:
Where is the size of the s string.
Minimum Window Substring
The problem description can be found in LeetCode.
Approach
From the title we already know that we have a Sliding Window problem.
In particular, this is a Sliding Window with a Dynamic Size problem.
In fact, the problem doesn't mention any static size to check, so we don't know about the actual size of the window.
The trick here is to find an efficient way to understand if the property of the window is fulfilled.
In this case, we need to be sure that all the characters of t are in s (duplicates included).
An efficient way to do so is to keep track of the matching characters. Hence, we will try to shrink the window as soon as we have the same number of matching characters.
This value is simply equal to the size of the counter dictionary that we will create for the string t.
Solution
from collections import defaultdict
from typing import DefaultDict
class Solution:
def minWindow(self, s: str, t: str) -> str:
if len(t) > len(s):
return ""
t_counter: DefaultDict[str, int] = self.get_chars_counter(t)
required_chars = len(t_counter)
left = 0
matching_chars = 0
s_counter: DefaultDict[str, int] = defaultdict(int)
ans = ""
for right, char in enumerate(s):
# the current char is not in `t`
# hence, we can avoid to consider it
if char not in t_counter:
continue
s_counter[char] += 1
# incrementing the `matching_chars` once the number of occurrences
# for `char` is equal in both counters
if s_counter[char] == t_counter[char]:
matching_chars += 1
# shrink if we have the same number of matching characters
while left <= right and matching_chars == required_chars:
left_char = s[left]
win_size = right - left + 1
# update the solution
if not ans or win_size < len(ans):
ans = s[left : right + 1]
# be sure that the `left_char` is in the `t` string,
# otherwise we risk to consider unused chars
if left_char in t_counter:
s_counter[left_char] -= 1
# decrease the `matching_chars` once `s_counter`
# does not contain enough for matching `t`
if s_counter[left_char] < t_counter[left_char]:
matching_chars -= 1
left += 1
return ans
def get_chars_counter(self, s: str) -> DefaultDict[str, int]:
counter: DefaultDict[str, int] = defaultdict(int)
for char in s:
counter[char] += 1
return counter
Complexity
- Time:
- Space:
Where and are the size of the strings and , respectively.
Regarding the space, the alphabet is limited to 56 characters,
therefore it is constant.
Maximum Profit in Job Scheduling
The problem description can be found in LeetCode.
Approach
An easy way to think about this problem would be reason on how we should select or discard a certain job.
What if we try every possibility?
We can either select the first job or discard it. Then, for both choices, we can again select the second job or discard it.
This decision tree and a possible repeating work in checking this options suggest to apply Dynamic Programming.
However, we need an efficient way for selecting the next job that we might select or discard. Usually, for these kind of problems, sorting the input is highly recommended, since any other brute force approach would have surely a higher complexity compared to .
Again, sorting the input suggests that Binary Search might be used. In fact, in order to select the next job, we can use it to quickly find it.
Solution
import bisect
from typing import Dict, List
class Solution:
def jobScheduling(
self, startTimes: List[int], endTimes: List[int], profits: List[int]
) -> int:
def dfs(i: int, memo: Dict[int, int]) -> int:
if i >= len(startTimes):
return 0
if i in memo:
return memo[i]
next_pos = bisect.bisect_left(startTimes, endTimes[i])
profit = max(
dfs(i + 1, memo),
profits[i] + dfs(next_pos, memo),
)
memo[i] = profit
return memo[i]
# sort the lists based on the `startTimes` one
combined = list(zip(startTimes, endTimes, profits))
sorted_combined = sorted(combined, key=lambda lst: lst[0])
startTimes = [v[0] for v in sorted_combined]
endTimes = [v[1] for v in sorted_combined]
profits = [v[2] for v in sorted_combined]
return dfs(0, {})
Complexity
- Time:
- Space:
Where is the size of the three input lists.
Merge Two Sorted Lists
The problem description can be found in LeetCode.
Approach
It is very easy to think on a recursive approach here. In fact, we should take:
list1[0]+merge(list1[1:], list2)iflist1[0] < list2[0].list2[0]+merge(list1, list2[1:])iflist1[0] >= list2[0].
Solution
from typing import Optional
class Solution:
def mergeTwoLists(
self, list1: Optional[ListNode], list2: Optional[ListNode]
) -> Optional[ListNode]:
if not list1 and not list2:
return None
if not list1:
return list2
if not list2:
return list1
if list1.val < list2.val:
list1.next = self.mergeTwoLists(list1.next, list2)
return list1
else:
list2.next = self.mergeTwoLists(list1, list2.next)
return list2
Complexity
- Time:
- Space:
Where and are the sizes of the list1 and list2 lists, respectively.
Linked List Cycle
The problem description can be found in LeetCode.
Approach
There are several ways to solve this problem and, as usual, we have to clarify the requirements with the interviewer.
- Iterate over the Linked List and add the node value to a Set. If the value is already in the set, then it means that there is a cycle. This would require time and space. However, this would assume that no value is duplicated unless the cycle is present.
- Another technique consists of applying the Floyd's tortoise and hare algorithm. We would keep two pointers: one moves by one step and one moves by two steps. If there is a cycle, the two pointers will meet at some point.
Solution
from typing import Optional
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
slow = head
fast = head.next if head else None
while fast and fast.next:
if slow == fast:
return True
slow = slow.next
fast = fast.next.next
return False
Complexity
- Time:
- Space:
Where is the size of the linked list.
Reverse Linked List
The problem description can be found in LeetCode.
Approach
It is enough to keep track of two consecutive pointers.
At each iteration, we reverse direction of each node's next pointer.
In particular, p is used for keeping track of the new head,
whereas q traverse the list.
Solution
from typing import Optional
class Solution:
def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
p, q = None, head
while q:
q_next = q.next
q.next = p
p = q
q = q_next
return p
Complexity
- Time:
- Space:
Where is the size of the linked list.
Middle of the Linked List
The problem description can be found in LeetCode.
Approach
A naive approach would consist of storing all the nodes values to a classic list and
then returning the middle element.
However, this would require space, where is the number of nodes in the Linked Lists.
In order to use no additional space, we can apply the Floyd's tortoise and hare algorithm, that we already applied in the Linked List Cycle problem.
Solution
from typing import Optional
class Solution:
def middleNode(self, head: Optional[ListNode]) -> Optional[ListNode]:
slow = fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
return slow
Complexity
- Time:
- Space:
Where is the size of the nums list.
LRU Cache
The problem description can be found in LeetCode.
Approach
This is a great article that explains the design behind a LRU cache. Most of the code below is taken from the same article.
Solution
from collections import OrderedDict
from typing import OrderedDict
class LRUCache:
def __init__(self, capacity: int) -> None:
self.capacity = capacity
self.cache: OrderedDict[int, int] = OrderedDict()
def get(self, key: int) -> int:
if key not in self.cache:
return -1
self.cache.move_to_end(key)
return self.cache[key]
def put(self, key: int, value: int) -> None:
if key in self.cache:
self.cache[key] = value
self.cache.move_to_end(key)
return
if len(self.cache) >= self.capacity:
lru_key = next(iter(self.cache))
del self.cache[lru_key]
self.cache[key] = value
Complexity
- Time:
- Space:
References
Valid Parentheses
The problem description can be found in LeetCode.
Approach
This is a classic problem to use a Stack. The idea is also quite intuitive.
Every time we see an open parenthesis, we can push the corresponding closed one in the stack. On the other hand, if the current parenthesis is a closed one, we check the top of the stack and if it is empty or it does not correspond, the string is not valid; otherwise, we continue with the next character.
Solution
class Solution:
def isValid(self, s: str) -> bool:
m = {
"}": "{",
"]": "[",
")": "(",
}
open_pars = set(m.values())
stack = []
for char in s:
if char in open_pars:
stack.append(char)
else:
if not stack:
return False
if stack.pop() != m[char]:
return False
return len(stack) == 0
Complexity
- Time:
- Space:
Where is the size of the s list.
Implement Queue using Stacks
The problem description can be found in LeetCode.
Approach
Suppose that we need to make a lot of push operations.
After doing so, the first element that is in the stack (we are forced to use a stack as data structure) is at the bottom.
So we cannot directly access it, since there is no stack operation that allows us to do it.
In fact, we cannot use any index (as for the requirements).
Now, suppose that we have the same number of pop operations.
We know that we must use another stack (as for the requirements),
so we can use the other stack to store the values we have to pop.
If we pop from the first stack and we push to the second one,
magically the actual order is restored,
we can start to return the values from the second stack.
Let's take an example:
obj = MyQueue()
obj.push(1)
obj.push(2)
obj.push(3)
obj.push(4)
# `obj.stack_1` would be
#
# | 4 |
# | 3 |
# | 2 |
# | 1 |
# |___|
Now, let's make a single pop operation and move all the elements to the other stack:
obj = MyQueue()
_ = obj.pop()
# `obj.stack_2` would be
#
# | 1 |
# | 2 |
# | 3 |
# | 4 |
# |___|
So if we pop from obj.stack_2 we can get the proper order.
Solution
from typing import List
class MyQueue:
def __init__(self) -> None:
self.stack_push: List[int] = []
self.stack_pop: List[int] = []
def push(self, x: int) -> None:
self.stack_push.append(x)
def pop(self) -> int:
if self.stack_pop:
return self.stack_pop.pop()
self._reorganize_stacks()
return self.pop()
def peek(self) -> int:
if self.stack_pop:
return self.stack_pop[-1]
self._reorganize_stacks()
return self.peek()
def empty(self) -> bool:
return not self.stack_push and not self.stack_pop
def _reorganize_stacks(self) -> None:
assert not self.stack_pop
assert self.stack_push
while self.stack_push:
self.stack_pop.append(self.stack_push.pop())
Complexity
For the single operation, we would have the following complexities:
push:- Time:
- Space:
pop:- Time:
- Space:
peek:- Time:
- Space:
empty:- Time:
- Space:
Evaluate Reverse Polish Notation
The problem description can be found in LeetCode.
Approach
As for Valid Parentheses, a Stack can be used used to keep track of intermediate results.
In fact, as soon as we encounter an operator, we can assume that the stack contains at least 2 elements (based on Reverse Polish Notation definition) and proceed to apply the operator to the two numbers. The result will be at the top of the stack.
Solution
from typing import List
class Solution:
def evalRPN(self, tokens: List[str]) -> int:
ops = {"+", "-", "*", "/"}
stack: List[int] = []
for token in tokens:
if token in ops:
assert len(stack) > 1, f"{stack} ({len(stack)})"
num2 = stack.pop()
num1 = stack.pop()
if token == "+":
stack.append(num1 + num2)
elif token == "-":
stack.append(num1 - num2)
elif token == "*":
stack.append(num1 * num2)
elif token == "/":
stack.append(int(num1 / num2))
else:
stack.append(int(token))
assert len(stack) == 1, f"{stack} ({len(stack)})"
return stack[-1]
Complexity
- Time:
- Space:
Where is the size of the tokens list.
Min Stack
The problem description can be found in LeetCode.
Approach
The idea here is to keep two stacks.
One will be used to keep every value that goes into the push method.
The second one will be used to keep only the minimum values instead.
Solution
class MinStack:
def __init__(self):
self.stack = []
self.min_stack = []
def push(self, val: int) -> None:
self.stack.append(val)
if not self.min_stack or self.getMin() >= val:
self.min_stack.append(val)
def pop(self) -> None:
val = self.stack.pop()
if self.getMin() == val:
_ = self.min_stack.pop()
def top(self) -> int:
return self.stack[-1]
def getMin(self) -> int:
return self.min_stack[-1]
Complexity
For the single operation, we would have the following complexities:
push:- Time:
- Space:
pop:- Time:
- Space:
top:- Time:
- Space:
getMin:- Time:
- Space:
Trapping Rain Water
The problem description can be found in LeetCode.
Approach
An easy way to think about this problem is to first understand how much water a single location can contain.
For each position, the amount of water is bounded to the minimum value between the maximum height on the left and on the right, minus its height.
In fact, think of a single cell of height 0 with their corresponding maximum left and right heights equal to n.
That cell can contain n - h = n - 0 = n amount of water.
So, a naive implementation would consist of calculating the maximum left and right and then calculate the amount of trapped water by summing up all the water that can be contained in every cell:
from typing import List
class Solution:
def trap(self, heights: List[int]) -> int:
max_left = [0] * len(heights)
max_right = [0] * len(heights)
ml = 0
for i in range(len(heights)):
max_left[i] = ml
ml = max(ml, heights[i])
mr = 0
for i in range(len(heights) - 1, -1, -1):
max_right[i] = mr
mr = max(mr, heights[i])
ans = 0
for i in range(len(heights)):
trapped_water = min(max_left[i], max_right[i]) - heights[i]
ans += max(trapped_water, 0)
return ans
This would require for both time and space.
However, there is a better approach, which does not require this additional space. In fact, we only care about finding a higher height either on left or right for the single cell.
At every cell, if we increment the left pointer, it means that there is a higher height on the right. Alternatively, we could increment the right one if the left pointer points to a higher height value.
This means that we do not actually care about higher height which is either on the left or on the right. We just know that there is one, which means that the cell could contain some water.
Solution
from typing import List
class Solution:
def trap(self, heights: List[int]) -> int:
left, right = 0, len(heights) - 1
left_max, right_max = heights[left], heights[right]
ans = 0
while left < right:
if left_max < right_max:
# there is a higher height on the `right`,
# which means that the `left` pointer contains
# a smaller value
#
# this would be an implicit `min(max_left[i], max_right[i])`
# as we did in the previous implementation
left += 1
left_max = max(left_max, heights[left])
ans += left_max - heights[left]
else:
# check the considerations above
right -= 1
right_max = max(right_max, heights[right])
ans += right_max - heights[right]
return ans
Complexity
- Time:
- Space:
Where is the size of the heights list.
Basic Calculator
The problem description can be found in LeetCode.
Approach
Solution
class Solution:
def calculate(self, s: str) -> int:
stack = []
num = res = 0
sign = 1
i = 0
while i < len(s):
char = s[i]
if char.isdigit():
j = i
while i < len(s) and s[i].isdigit():
i += 1
num = int(s[j:i])
continue
if char == "+" or char == "-":
res += sign * num
sign = 1 if char == "+" else -1
num = 0
elif char == "(":
stack.append(res)
stack.append(sign)
sign = 1
res = 0
elif char == ")":
assert len(stack) > 1
res += sign * num
res *= stack.pop()
res += stack.pop()
num = 0
i += 1
return res + (sign * num)
Complexity
- Time:
- Space:
Where is the size of the nums list.
Largest Rectangle in Histogram
The problem description can be found in LeetCode.
Approach
This is a classic problem that can be solved by checking all the possible areas between each pair of the input array. This would require time and space.
For these kind of problems, usually, we can drop the time to by using a data structure, which can store some intermediate results. In particular, for this problem, we could use a Monotonic Stack.
Let's take a look at some examples:
| |
| | |
2 1 2
In the case above,
the first element 2 is bounded to the second element 1.
In fact, the maximum height we can obtain from the two is the minimum one.
We can include the 2 in the area calculation, but the height would be 1.
So, we just need to keep the base from 2 (index 0) and consider the height of 1 (index 1).
Then, once we reach the 2,
we can calculate the area by having a base as 3 (2-index - 0-index + 1) and
a height as 1.
An edge case would be something like:
| | |
| | |
2 2 2
This is not a monotonic increase sequence.
However, we could insert a fake height of 0 in the end to consume all possible heights that are in the stack:
| | |
| | |
2 2 2 0
Solution
from itertools import chain
from typing import List, Tuple
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
ans = 0
stack: List[Tuple[int, int]] = []
for i, height in enumerate(chain(heights, [0])):
start = i
while stack and stack[-1][1] > height:
curr_i, curr_height = stack.pop()
ans = max(ans, curr_height * (i - curr_i))
start = curr_i
stack.append((start, height))
return ans
Complexity
- Time:
- Space:
Where is the size of the heights list.
Invert Binary Tree
The problem description can be found in LeetCode.
Approach
This is our first Tree problem. They can be quite tricky at first and it takes time to master them.
What can we notice from the examples?
Surely, the root node remains the same, which means that we must return the root node itself, but we have to apply some logic before.
This logic is quite simple: just switch the left and right,
and, after doing so, we can apply the same logic recursively to the children nodes.
Solution
from typing import Optional
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return None
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
Complexity
- Time:
- Space:
Where is the number of nodes in the tree and is its height. If the tree is unbalanced, it is like having a Linked List, hence .
Maximum Depth of Binary Tree
The problem description can be found in LeetCode.
Approach
This is a classic Tree problem and such pattern is very important to understand for solving other problems.
Here, we simply calculate the left and right depth and return the maximum between them.
The same is applied to all the node, recursively.
Solution
from typing import Optional
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
left_depth = self.maxDepth(root.left)
right_depth = self.maxDepth(root.right)
return 1 + max(left_depth, right_depth)
Complexity
- Time:
- Space:
Where is the number of nodes in the tree and is its height. If the tree is unbalanced, it is like having a Linked List, hence .
Lowest Common Ancestor of a Binary Search Tree
The problem description can be found in LeetCode.
Approach
The problem states that the Tree that we take as input is a Binary Search Tree. So we surely have to take this into consideration for our final algorithm. We have to take advantage of this property to derive our solution.
One thing we can notice here is that if the nodes we are looking for are in different sub-trees,
then, the LCA is the root node itself.
However, if they belong to the same sub-tree, it means that both nodes are either
fewer (left sub-tree) or greater (right sub-tree) than the node itself.
So we can recursively continue our search on the proper sub-tree.
Solution
class Solution:
def lowestCommonAncestor(
self, root: TreeNode, p: TreeNode, q: TreeNode
) -> TreeNode:
lca = root
while lca:
if p.val > lca.val and q.val > lca.val:
lca = lca.right
elif p.val < lca.val and q.val < lca.val:
lca = lca.left
else:
break
return lca
Complexity
- Time:
- Space:
Where is the height of the tree. If the tree is unbalanced, it is like having a Linked List, hence .
Balanced Binary Tree
The problem description can be found in LeetCode.
Approach
A trick is to use a magic value -1 to mark a sub-tree as unbalanced.
In this way, we can avoid to return both height and a possible boolean value,
which could indicate if the tree is unbalanced or not.
In any case, both solutions are valid and they have the same space and time complexities
Solution
from typing import Optional
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def dfs(root: Optional[TreeNode]) -> int:
if not root:
return 0
left_height = dfs(root.left)
right_height = dfs(root.right)
diff_heights = abs(left_height - right_height)
if left_height == -1 or right_height == -1 or diff_heights > 1:
return -1
return 1 + max(left_height, right_height)
return dfs(root) != -1
from typing import Optional, Tuple
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def dfs(root: Optional[TreeNode]) -> Tuple[int, bool]:
if not root:
return 0, True
left_height, left_balanced = dfs(root.left)
right_height, right_balanced = dfs(root.right)
height = 1 + max(left_height, right_height)
if not left_balanced or not right_balanced:
return height, False
diff_heights = abs(left_height - right_height)
is_balanced = diff_heights <= 1
return height, is_balanced
_, is_balanced = dfs(root)
return is_balanced
Complexity
- Time:
- Space:
Where is the number of nodes in the tree and is its height. If the tree is unbalanced, it is like having a Linked List, hence .
Diameter of Binary Tree
The problem description can be found in LeetCode.
Approach
The same considerations made for the Balanced Binary Tree problem apply here.
For this problem, we can simply calculate every possible diameter. In order to do so, it is enough to calculate it for every node of the tree and keep track of the maximum value, which will be our result.
However, in this case I want to show how it possible to return multiple values from the recursive function. An alternative approach would consist of having a global variable to keep track of the maximum diameter.
Solution
from typing import Optional, Tuple
class Solution:
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
def dfs(root: Optional[TreeNode]) -> Tuple[int, int]:
if not root:
return 0, 0
left_height, left_diameter = dfs(root.left)
right_height, right_diameter = dfs(root.right)
diameter = max(
left_height + right_height,
left_diameter,
right_diameter,
)
return 1 + max(left_height, right_height), diameter
_, diameter = dfs(root)
return diameter
Complexity
- Time:
- Space:
Where is the number of nodes in the tree and is its height. If the tree is unbalanced, it is like having a Linked List, hence .
Binary Tree Level Order Traversal
The problem description can be found in LeetCode.
Approach
This is a perfect example to apply BFS, since it is a level-by-level traversal by definition (first solution).
DFS can be applied too, but you also need to keep track of the current level (second solution).
Solution
from collections import deque
from typing import List, Optional
class Solution:
def levelOrder(self, root: Optional[TreeNode] = None) -> List[List[int]]:
if not root:
return []
queue = deque([root])
ans: List[List[int]] = []
level = 0
while queue:
ans.append([])
for _ in range(len(queue)):
node = queue.popleft()
ans[level].append(node.val)
for child in [node.left, node.right]:
if child:
queue.append(child)
level += 1
return ans
from collections import deque
from typing import List, Optional
class Solution:
def levelOrder(self, root: Optional[TreeNode] = None) -> List[List[int]]:
if not root:
return []
queue = deque([root])
ans: List[List[int]] = []
level = 0
while queue:
ans.append([])
for _ in range(len(queue)):
node = queue.popleft()
ans[level].append(node.val)
for child in [node.left, node.right]:
if child:
queue.append(child)
level += 1
return ans
Complexity
- Time:
- Space:
Where is the number of nodes in the tree.
Validate Binary Search Tree
The problem description can be found in LeetCode.
Approach
The solution is in the question itself. It already collects all the three checks we need to perform in the problem description.
So, once we checked the correctness of the root, left and right values,
we start checking all the other sub-trees.
Solution
from typing import Optional
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
def dfs(
root: Optional[TreeNode], lower_bound: float, upper_bound: float
) -> bool:
if not root:
return True
if not (lower_bound < root.val < upper_bound):
return False
return dfs(root.left, lower_bound, root.val) and dfs(
root.right, root.val, upper_bound
)
return dfs(root, float("-inf"), float("+inf"))
Complexity
- Time:
- Space:
Where is the number of nodes in the tree and is its height. If the tree is unbalanced, it is like having a Linked List, hence .
Lowest Common Ancestor of a Binary Tree
The problem description can be found in LeetCode.
Approach
Here, it is enough to draw some examples.
When we are in a certain node,
we can recursively check the values that point to p and q pointers on both left and right.
At this point,
we can have three possibilities:
- No nodes found. This means that we have to look at other nodes.
- We found one node at the
leftand one node at theright. This means that the current node is ourLCA. - We found either
leftorright. So, we can return the one we found.
Solution
from typing import Optional
class Solution:
def lowestCommonAncestor(
self, root: "TreeNode", p: "TreeNode", q: "TreeNode"
) -> "TreeNode":
def dfs(node: "TreeNode") -> Optional["TreeNode"]:
if not node:
return None
if node.val == p.val or node.val == q.val:
return node
left = dfs(node.left)
right = dfs(node.right)
if left and right:
return node
if left:
return left
if right:
return right
raise Exception("unreachable")
return dfs(root)
Complexity
- Time:
- Space:
Where is the number of nodes in the tree and is its height. If the tree is unbalanced, it is like having a Linked List, hence .
Binary Tree Right Side View
The problem description can be found in LeetCode.
Approach
Again, we have another example that perfectly adapts to DFS (like Binary Tree Level Order Traversal).
We will make a level order traversal and simply add the last one of the level in our result.
Solution
from collections import deque
from typing import Deque, List, Optional
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
queue: Deque[int] = deque()
if root:
queue.append(root)
ans = []
while queue:
ans.append(queue[-1].val)
for _ in range(len(queue)):
node = queue.popleft()
for child in [node.left, node.right]:
if child:
queue.append(child)
return ans
Complexity
- Time:
- Space:
Where is the number of nodes in the tree. If our input is a perfect binary tree, the maximum number of nodes that could be in the queue are the ones in the last level, which is , where is the height of the tree.
Construct Binary Tree from Preorder and Inorder Traversal
The problem description can be found in LeetCode.
Approach
As usual, we have to derive some examples to really understand how to solve a problem.
If we see the first one in the problem description, we can notice that:
preorder = [3, 9, 20, 15, 7]
inorder = [9, 3, 15, 20, 7]
The first 3 will be the actual root node in the tree and
we can find it in the preorder list.
Then, if we look for the node 3 in the inorder list,
we can notice that the elements on the:
leftare part of theleftsubtree ([9]).rightare part of therightsubtree ([15, 20, 7]).
If we apply the same logic again recursively, we can see that this also applies to all the other nodes.
We can apply such properties to the code too.
Solution
from typing import List, Optional
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
assert len(preorder) == len(inorder)
if not preorder:
return None
val = preorder[0]
node = TreeNode(val)
n = inorder.index(val)
node.left = self.buildTree(preorder[1 : n + 1], inorder[:n])
node.right = self.buildTree(preorder[n + 1 :], inorder[n + 1 :])
return node
Complexity
- Time:
- Space:
Where is the number of nodes in the tree
Kth Smallest Element in a BST
The problem description can be found in LeetCode.
Approach
Since we are looking for the k-th smallest element
in a Binary Search Tree, the smallest ones are on the left side.
In particular, if we follow the In-order traversal, we would get an ordered list of values.
In this traversal, the order is:
- Left.
- Node.
- Right.
We can use the 2. step to check the value of the node and
keep track of the answer in a global variable,
which we can update as soon as we found the k-th smallest element.
Here, we can either start from k and go until 0 (as implemented) or
start from 0 and go until k.
Solution
from typing import Optional
class Solution:
def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
def dfs(node: Optional[TreeNode]) -> None:
nonlocal ans
nonlocal i
if not node:
return
dfs(node.left)
i -= 1
if i == 0:
ans = node.val
else:
dfs(node.right)
ans = -1
i = k
dfs(root)
assert ans != -1, "expected one solution"
return ans
Complexity
- Time:
- Space:
Where is the number of nodes in the tree and is its height. If the tree is unbalanced, it is like having a Linked List, hence .
Serialize and Deserialize Binary Tree
The problem description can be found in LeetCode.
Approach
We can use DFS to serialize all the nodes and deserialize them back to get the original tree.
For the following tree:
We would need to generate a string like:
[1, 2, 4, 5, 3, 6, 7]
As you can see,
we will prioritize the nodes on the left sub-tree and
then proceed with the ones onthe right.
Solution
from typing import List, Optional, Tuple
class Codec:
NULL_NODE = "null"
NODE_SEP = ","
def serialize(self, root: Optional[TreeNode]) -> str:
def dfs(node: Optional[TreeNode], nodes) -> None:
if not node:
nodes.append(Codec.NULL_NODE)
else:
nodes.append(str(node.val))
dfs(node.left, nodes)
dfs(node.right, nodes)
nodes: List[str] = []
dfs(root, nodes)
return Codec.NODE_SEP.join(nodes)
def deserialize(self, data: str) -> Optional[TreeNode]:
def dfs(i: int) -> Tuple[int, Optional[TreeNode]]:
if nodes[i] == Codec.NULL_NODE:
i += 1
return i, None
node = TreeNode(nodes[i])
i += 1
i, left_node = dfs(i)
i, right_node = dfs(i)
node.left = left_node
node.right = right_node
return i, node
i = 0
nodes = data.split(Codec.NODE_SEP)
_, root = dfs(i)
return root
Complexity
- Time:
- Space:
Where is the number of nodes in the tree.
Implement Trie (Prefix Tree)
We have already covered this problem in the Trie section.
Flood Fill
The problem description can be found in LeetCode.
Approach
Sometimes Graph problems are hidden by other representations. In fact, the input matrix we can find in the first example can be thought as a Graph.
In this case, we don't need to derive any Adjacency List.
In fact, we can directly calculate the neighbors by getting the values directly connected at the top, bottom, left and right.
Once we get the neighbors, we could add them to a Stack and process them later if their color matches the one at [sr][sc].
Solution
from typing import List
class Solution:
def floodFill(
self, image: List[List[int]], sr: int, sc: int, color: int
) -> List[List[int]]:
old_color = image[sr][sc]
if old_color == color:
return image
rows, cols = len(image), len(image[0])
stack = [(sr, sc)]
deltas = [
(-1, 0), # up
(+1, 0), # down
(0, -1), # left
(0, +1), # right
]
while stack:
row, col = stack.pop()
image[row][col] = color
for d_row, d_col in deltas:
new_row = row + d_row
new_col = col + d_col
if (
0 <= new_row < rows
and 0 <= new_col < cols
and image[new_row][new_col] == old_color
):
stack.append((new_row, new_col))
return image
Complexity
- Time:
- Space:
Where and are the number of rows and columns of the input image, respectively.
01 Matrix
The problem description can be found in LeetCode.
Approach
This is another example of an implicit Graph, as the Flood Fill problem we saw earlier.
The problem looks like a usual BFS one,
since it would be enough to search at the nearest 0 if the cell is not equal to 0.
However, if we imagine an input like:
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 0
We would need to make a BFS times,
which is .
A smarter way would be to build the result matrix from scratch.
We can initialize our queue with only coordinates of 0 values.
Then, we can perform a BFS algorithm to update the distances of the cells that are not equal to 0.
Solution
from collections import deque
from typing import Deque, Iterator, List, Set, Tuple
class Solution:
def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
# not ideal, but just to avoid to have too many function parameters
self.mat = mat
self.rows, self.cols = len(mat), len(mat[0])
visited = set()
queue: Deque[Tuple[int, int]] = deque()
for row in range(self.rows):
for col in range(self.cols):
if self.mat[row][col] == 0:
visited.add((row, col))
queue.append((row, col))
self.bfs(row, col, queue, visited)
return self.mat
def bfs(
self,
row: int,
col: int,
queue: Deque[Tuple[int, int]],
visited: Set[Tuple[int, int]],
) -> None:
distance = 0
while queue:
for _ in range(len(queue)):
row, col = queue.popleft()
self.mat[row][col] = distance
for nbr_row, nbr_col in self.get_neighbors(row, col):
if (nbr_row, nbr_col) in visited:
continue
visited.add((nbr_row, nbr_col))
queue.append((nbr_row, nbr_col))
distance += 1
def get_neighbors(self, row: int, col: int) -> Iterator[Tuple[int, int]]:
deltas = [
(-1, 0), # up
(+1, 0), # down
(0, -1), # left
(0, +1), # right
]
for dt_row, dt_col in deltas:
nbr_row = row + dt_row
nbr_col = col + dt_col
if (
0 <= nbr_row < self.rows
and 0 <= nbr_col < self.cols
and self.mat[nbr_row][nbr_col] != 0
):
yield nbr_row, nbr_col
Complexity
- Time:
- Space:
Where and are the number of rows and columns of the input matrix, respectively.
Clone Graph
The problem description can be found in LeetCode.
Approach
In this problem, we just need a way to traverse the Graph, and then clone the current node, plus its children.
However, we need to be careful about possible cycles.
In fact, if we have a simple Undirected Graph with two nodes,
we need a way to keep track of the first node we have already cloned.
Otherwise, when we try to clone the neighbors of the second node,
we would visit the first node again.
We can keep track of a mapping between the old nodes and the new ones. In this way, we can simply return the node we have already cloned if it is processed twice.
Solution
from typing import Dict, Optional
class Solution:
def cloneGraph(self, node: Optional["Node"]) -> Optional["Node"]:
def dfs(
node: Optional["Node"], old_to_new: Dict["Node", "Node"]
) -> Optional["Node"]:
if not node:
return None
if node in old_to_new:
return old_to_new[node]
new_node = Node(node.val, [])
old_to_new[node] = new_node
for neighbor in node.neighbors:
new_node.neighbors.append(dfs(neighbor, old_to_new))
return new_node
return dfs(node, {})
Complexity
- Time:
- Space:
Where and are the number of edges and vertices of the input graph, respectively.
Course Schedule
The problem description can be found in LeetCode.
Approach
This is a typical problem where we can apply Topological Sorting algorithm. In particular, if a topological ordering is possible it means that the student can finish all the courses.
Moreover, we can also notice that the input is not a Graph, but we can easily build an Adjacency List.
Solution
from collections import deque
from typing import Deque, Dict, List
class Solution:
def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
graph = self.get_adjacency_list(numCourses, prerequisites)
in_degree = self.get_in_degree(graph)
queue: Deque[int] = deque()
for course, degree in in_degree.items():
if degree == 0:
queue.append(course)
num_checked_courses = 0
while queue:
course = queue.popleft()
num_checked_courses += 1
for dep_course in graph[course]:
in_degree[dep_course] -= 1
if in_degree[dep_course] == 0:
queue.append(dep_course)
return num_checked_courses == numCourses
def get_adjacency_list(
self, numCourses: int, prerequisites: List[List[int]]
) -> Dict[int, List[int]]:
graph: Dict[int, List[int]] = {course: [] for course in range(numCourses)}
for a, b in prerequisites:
graph[b].append(a)
return graph
def get_in_degree(self, graph: Dict[int, List[int]]) -> Dict[int, int]:
in_degree: Dict[int, int] = {course: 0 for course in range(len(graph))}
for course_preqs in graph.values():
for course in course_preqs:
in_degree[course] += 1
return in_degree
Complexity
- Time:
- Space:
Where is the size of the prerequisites list.
Number of Islands
The problem description can be found in LeetCode.
Approach
This is a classic and it can be solved with both DFS and BFS.
I personally prefer the recursive DFS approach,
which is the one that uses less code.
Here, we assume that the input can be changed,
so we do not need to keep a visited Set to track the already seen coordinates.
However, this is something we need to clarify with the interviewer.
Solution
from typing import List
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
# not ideal, but just to avoid to have too many function parameters
self.grid = grid
self.rows, self.cols = len(grid), len(grid[0])
ans = 0
for row in range(self.rows):
for col in range(self.cols):
if grid[row][col] == "1":
self.dfs(row, col)
ans += 1
return ans
def dfs(self, row: int, col: int) -> None:
if (
not (0 <= row < self.rows and 0 <= col < self.cols)
or self.grid[row][col] == "0"
):
return
self.grid[row][col] = "0"
self.dfs(row - 1, col) # up
self.dfs(row + 1, col) # down
self.dfs(row, col - 1) # left
self.dfs(row, col + 1) # right
Complexity
- Time:
- Space:
Where and are the number of rows and columns of the input grid, respectively.
Rotting Oranges
The problem description can be found in LeetCode.
Approach
From the input images, it is clear that this is a BFS problem. In fact, at every minute, the rotten oranges could expand at the usual four directions as a single step. This looks like a breadth expansion.
As usual, this is not a clearly implicit Graph problem, but a matrix can be easily adapted to it.
As for 01 Matrix, we can first initialize our queue with the rotten oranges, and then we can expand them by single steps. In the end, if the amount of rotten oranges (from minute 1 on) is equal to the original number of the fresh oranges, then it means that there is not a fresh orange left, so we can return the elapsed time (number of minutes).
Solution
from collections import deque
from enum import Enum
from typing import Deque, Iterator, List, Tuple
class Orange(Enum):
NONE = 0
FRESH = 1
ROTTEN = 2
class Solution:
def orangesRotting(self, grid: List[List[int]]) -> int:
# not ideal, but just to avoid to have too many function parameters
self.grid = grid
self.rows, self.cols = len(grid), len(grid[0])
num_fresh_oranges = 0
queue: Deque[Tuple[int, int]] = deque()
for row in range(self.rows):
for col in range(self.cols):
if grid[row][col] == Orange.FRESH.value:
num_fresh_oranges += 1
elif grid[row][col] == Orange.ROTTEN.value:
queue.append((row, col))
num_rotten_oranges, minutes = self.bfs(queue)
return minutes if num_fresh_oranges == num_rotten_oranges else -1
def bfs(self, queue: Deque[Tuple[int, int]]) -> Tuple[int, int]:
minutes = 0
num_rotten_oranges = 0
while queue:
for _ in range(len(queue)):
row, col = queue.popleft()
for nbr_row, nbr_col in self.get_neighbors(row, col):
self.grid[nbr_row][nbr_col] = Orange.ROTTEN.value
queue.append((nbr_row, nbr_col))
num_rotten_oranges += 1
if queue:
minutes += 1
return num_rotten_oranges, minutes
def get_neighbors(self, row: int, col: int) -> Iterator[Tuple[int, int]]:
deltas = [
(-1, 0), # up
(+1, 0), # down
(0, -1), # left
(0, +1), # right
]
for dt_row, dt_col in deltas:
nbr_row = row + dt_row
nbr_col = col + dt_col
if (
0 <= nbr_row < self.rows
and 0 <= nbr_col < self.cols
and self.grid[nbr_row][nbr_col] == Orange.FRESH.value
):
yield nbr_row, nbr_col
Complexity
- Time:
- Space:
Where and are the number of rows and columns of the input grid, respectively.
Accounts Merge
The problem description can be found in LeetCode.
Approach
This is an implicit Graph problem. In particular, we need to find a way to connect these emails based on some logic.
In fact, at first, we don't care about the name of the account. We just want to group these emails. Eventually, each group of emails will belong to a certain account.
First, we build the Adjacency List based on the emails. Secondly, we perform a DFS to iterate over this sub-groups.
Solution
from collections import defaultdict
from typing import DefaultDict, List, Set
class Solution:
def accountsMerge(self, accounts: List[List[str]]) -> List[List[str]]:
graph = self.get_adjacency_list(accounts)
return self.group_emails(accounts, graph)
def get_adjacency_list(
self, accounts: List[List[str]]
) -> DefaultDict[str, List[str]]:
graph = defaultdict(list)
for account in accounts:
emails = account[1:]
assert len(emails) > 0
first_email = emails[0]
for email in emails[1:]:
graph[first_email].append(email)
graph[email].append(first_email)
return graph
def group_emails(
self, accounts: List[List[str]], graph: DefaultDict[str, List[str]]
) -> List[List[str]]:
visited: Set[str] = set()
ans = []
for account in accounts:
name = account[0]
first_email = account[1]
if first_email in visited:
continue
emails: List[str] = []
self.dfs(graph, first_email, emails, visited)
emails.sort()
ans.append([name] + emails)
return ans
def dfs(
self,
graph: DefaultDict[str, List[str]],
email: str,
emails: List[str],
visited: Set[str],
) -> None:
if email in visited:
return
visited.add(email)
emails.append(email)
for neighbor in graph[email]:
self.dfs(graph, neighbor, emails, visited)
Complexity
- Time:
- Space:
Where and are the number of accounts and the maximum length of a certain account, respectively.
Word Search
The problem description can be found in LeetCode.
Approach
This is a classic Graph problem. Both BFS and DFS can be applied for this problem. However, usually, the DFS recursive implementation is less verbose and easier to implement.
As soon as we see a matching character, we can start our DFS to all the other characters of the string.
Then, we just need to mark the visited ones.
We can either have a visited Set or change the input board.
We could also revert the change after the search is complete,
since it is a operation.
Solution
from typing import List
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
# not ideal, but just to avoid to have too many function parameters
self.board = board
self.rows, self.cols = len(board), len(board[0])
for row in range(self.rows):
for col in range(self.cols):
if board[row][col] == word[0] and self.dfs(word, row, col):
return True
return False
def dfs(self, word: str, row: int, col: int) -> bool:
if not word:
return True
if not (0 <= row < self.rows and 0 <= col < self.cols):
return False
if self.board[row][col] != word[0]:
return False
# mark the current cell as `visited`
tmp = self.board[row][col]
self.board[row][col] = ""
ans = (
self.dfs(word[1:], row - 1, col) # up
or self.dfs(word[1:], row + 1, col) # down
or self.dfs(word[1:], row, col - 1) # left
or self.dfs(word[1:], row, col + 1) # right
)
# restore original value of the cell
self.board[row][col] = tmp
return ans
Complexity
- Time:
- Space:
Where , and are the number of rows and columns of the input board and the string word, respectively.
Minimum Height Trees
The problem description can be found in LeetCode.
Approach
Our input Tree is given as a list of edges as input. Hence, we can build a Graph by building an Adjacency List from these edges.
Another thing to consider is that this graph doesn't contain cycles. Moreover, there is just a single path between any two nodes of the Graph itself.
So, if we think about our input Tree as a skewed one, the internal nodes would have the minimum height if rooted, whereas the leaf nodes would have the maximum one.
Based on this assumption, we can design an algorithm to look for such internal nodes in the skewed tree, which would give us the minimum height.
Solution
from collections import deque
from typing import Deque, Dict, List
class Solution:
def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
assert n > 0
if n == 1:
return [0]
if n == 2:
return [0, 1]
graph = self.get_adjacency_list(n, edges)
return self.topological_sort(n, graph)
def get_adjacency_list(
self, n: int, edges: List[List[int]]
) -> Dict[int, List[int]]:
graph: Dict[int, List[int]] = {i: [] for i in range(n)}
for a, b in edges:
graph[a].append(b)
graph[b].append(a)
return graph
def topological_sort(self, n: int, graph: Dict[int, List[int]]) -> List[int]:
queue: Deque[int] = deque([])
# add leaf nodes
for node, neighbors in graph.items():
if len(neighbors) == 1:
queue.append(node)
not_processed_nodes = n
while not_processed_nodes > 2:
not_processed_nodes -= len(queue)
for _ in range(len(queue)):
node = queue.popleft()
neighbor = graph[node].pop()
graph[neighbor].remove(node)
# the node is now a leaf one
if len(graph[neighbor]) == 1:
queue.append(neighbor)
return list(queue)
Complexity
- Time:
- Space:
Where is the number of nodes in the graph.
Word Ladder
The problem description can be found in LeetCode.
Approach
Again, we have another form of implicit Graph,Graph.
Once we build our adjacency list,
we can perform a simple BFS starting from beginWord to endWord.
A BFS traversal will help us in calculating the minimum path between these two nodes (if any).
The tricky part would be to derive or Adjacency List.
In fact, assuming that all the strings in wordList have the same length,
we can consider two strings to be neighbors if they differ only by one character at most.
Building such Adjacency List would require ,
where is the size of wordList and is the unique length of each word in wordList
(as per the problem requirements).
from collections import deque
from typing import Dict, List, Tuple
class Solution:
def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
graph = self.get_adjacency_list(beginWord, wordList)
return self.bfs(graph, beginWord, endWord)
def bfs(self, graph: Dict[str, List[str]], beginWord: str, endWord: str) -> int:
queue = deque([beginWord])
visited = {beginWord}
ans = 1
while queue:
for _ in range(len(queue)):
node = queue.popleft()
if node == endWord:
return ans
for neighbor in graph[node]:
if neighbor in visited:
continue
queue.append(neighbor)
visited.add(neighbor)
ans += 1
return 0
def get_adjacency_list(
self, beginWord: str, wordList: List[str]
) -> Dict[str, List[str]]:
if beginWord not in wordList:
wordList.append(beginWord)
graph: Dict[str, List[str]] = {word: [] for word in wordList}
for i in range(len(wordList)):
word1 = wordList[i]
for j in range(i + 1, len(wordList)):
word2 = wordList[j]
diff_chars = sum(
int(char1 != char2) for char1, char2 in zip(word1, word2)
)
if diff_chars <= 1:
graph[word1].append(word2)
graph[word2].append(word1)
return graph
Although this approach is valid,
it is not enough to solve the problem in LeetCode.
In fact, we would get a Time Limit Exceeded error.
To overcome this solution, we have to think about a more optimized way to build the Adjacency List, which is the bottleneck of the previous approach.
A trick consists in using a pattern for each word. This pattern will be used as the key of the adjacency list and the value would be the actual string.
For example, for the beginWord hit we would have:
adj_list = {
"*it": "hit"
"h*t": "hit"
"hi*": "hit"
}
This would significantly reduce the complexity as per the requirements:
Solution
from collections import defaultdict, deque
from typing import Dict, Generator, List
class Solution:
def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
graph = self.get_adjacency_list(beginWord, wordList)
return self.bfs(graph, beginWord, endWord)
def bfs(self, graph: Dict[str, List[str]], beginWord: str, endWord: str) -> int:
queue = deque([beginWord])
visited = {beginWord}
ans = 1
while queue:
for _ in range(len(queue)):
word = queue.popleft()
if word == endWord:
return ans
for pattern in self.get_pattern_strings(word):
for neighbor in graph[pattern]:
if neighbor in visited:
continue
queue.append(neighbor)
visited.add(neighbor)
ans += 1
return 0
def get_adjacency_list(
self, beginWord: str, wordList: List[str]
) -> Dict[str, List[str]]:
if beginWord not in wordList:
wordList.append(beginWord)
graph = defaultdict(list)
for word in wordList:
for pattern in self.get_pattern_strings(word):
graph[pattern].append(word)
return graph
def get_pattern_strings(self, s: str) -> Generator[str, None, None]:
return (f"{s[:i]}*{s[i+1:]}" for i in range(len(s)))
Complexity
- Time:
- Space:
Where and are the length of wordList and the length of each string in wordList, respectively.
Combination Sum
The problem description can be found in LeetCode.
Approach
This is a classic problem where Backtracking can be applied.
In fact,
we can check all possible combination of numbers that will sum up to the target.
As soon as our current sum goes below 0,
it means that we can discard that path.
This is true because all numbers are between 2 and 40.
Solution
from typing import List
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
def dfs(i: int, amount: int, path: List[int], paths: List[List[int]]) -> None:
if amount == 0:
paths.append(path.copy())
return
if amount < 0 or i >= len(candidates):
return
for j in range(i, len(candidates)):
path.append(candidates[j])
dfs(j, amount - candidates[j], path, ans)
path.pop()
ans: List[List[int]] = []
dfs(0, target, [], ans)
return ans
Complexity
Let's consider the following example:
candidates = [1, 2, 5]
target = 5
This would produce the following space tree:
As for any DFS problem,
the space complexity will be proportional with the height of the tree,
which can be at most 5, hence .
Regarding the time complexity,
since the maximum height is ,
the maximum number of nodes in the tree is ,
where is the size of the candidates list.
Plus, we also need to consider the extra work we make to add a solution to the result list,
which is .
- Time:
- Space:
Where is .
Permutations
The problem description can be found in LeetCode.
Approach
This is a classic Backtracking problem.
We can again build our space tree and simply avoid to visit the same number twice.
Solution
from typing import List, Set
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
def dfs(seen: Set[int], curr: List[int], perms: List[List[int]]) -> None:
if len(curr) == len(nums):
perms.append(curr.copy())
return
for num in nums:
if num in seen:
continue
seen.add(num)
curr.append(num)
dfs(seen, curr, perms)
seen.remove(num)
curr.pop()
ans: List[List[int]] = []
dfs(set(), [], ans)
return ans
Complexity
- Time:
- Space:
Where is the size of the nums list.
Subsets
The problem description can be found in LeetCode.
Approach
As usual, the space tree is our friend:
At each step, we can either include the current element or exclude it (the x node).
Lastly, it will be enough to append each solution we find in each leaf node to build up the expected result.
Solution
from typing import List
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
def dfs(i: int, curr: List[int], subs: List[List[int]]) -> None:
if i == len(nums):
subs.append(curr.copy())
return
# include current element
curr.append(nums[i])
dfs(i + 1, curr, subs)
curr.pop()
# do not include current element
dfs(i + 1, curr, subs)
ans: List[List[int]] = []
dfs(0, [], ans)
return ans
Complexity
- Time:
- Space:
Where is the size of the nums list.
Letter Combinations of a Phone Number
The problem description can be found in LeetCode.
Approach
As usual, picturing a possible input is always a great choice.
In particular, assuming that we have an input like 23,
we would need to combine the strings abc for 2 and def for 3, respectively.
So, we could start by picking a first and combine it with every letter in def.
Then, we could do the same with b and then c.
This would require looping to every character and then build the result during the iteration itself.
However, here we do not know how many characters we can have.
So, we cannot simply loop over all possible characters with a simple chain of for loops.
For this reason, let's try to draw the space tree of this problem.
As you can see, every leaf node would contain a piece of our solution. We could simply concatenate the characters along that path to build it.
Besides adding characters along the path, we can also remove them once we explore them, hence applying a Backtracking approach.
Solution
from typing import List
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
def dfs(i: int, curr: List[str], combs: List[str]) -> None:
if i == len(digits):
if curr:
combs.append("".join(curr))
else:
for letter in mapping[digits[i]]:
curr.append(letter)
dfs(i + 1, curr, combs)
curr.pop()
mapping = {
"2": "abc",
"3": "def",
"4": "ghi",
"5": "jkl",
"6": "mno",
"7": "pqrs",
"8": "tuv",
"9": "wxyz",
}
ans: List[str] = []
dfs(0, [], ans)
return ans
Complexity
- Time:
- Space:
Where is the size of the digits list and
is the maximum size of characters that a digit might have.
In this case, .
Climbing Stairs
The problem description can be found in LeetCode.
Approach
For this problem,
a top-down approach comes very naturally.
Also because this looks like the Fibonacci one.
We can easily find out that the problem has repeated sub-problems, and we can use memoization to save their results.
Solution
from typing import Dict
class Solution:
def climbStairs(self, n: int) -> int:
def dfs(i: int, memo: Dict[int, int]) -> int:
assert i >= 0
if i in memo:
return memo[i]
if i == n:
return 1
if i > n:
return 0
memo[i] = dfs(i + 1, memo) + dfs(i + 2, memo)
return memo[i]
return dfs(0, {})
Complexity
- Time:
- Space:
Where is the number we take as input.
Maximum Subarray
The problem description can be found in LeetCode.
Approach
Here, we can apply the well-known Kadane's algorithm.
Solution
from typing import List
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
assert len(nums) > 0
best_sum = curr_sum = nums[0]
for num in nums[1:]:
curr_sum = max(num, curr_sum + num)
best_sum = max(best_sum, curr_sum)
return best_sum
Complexity
- Time:
- Space:
Where is the size of the nums list.
Coin Change
The problem description can be found in LeetCode.
Approach
A simple greedy approach would consist of start picking the coin with the highest values and then use the other ones.
Otherwise, this won't give us an optional solution for every input. In fact, suppose having this example:
coins = [5, 4, 1]
amount = 8
If we start from the most valuable coin, we would have [5, 1, 1, 1].
However, if we pick 4, we would have [4, 4].
So, a brute force approach would consist of checking all possible values that sum up to the target amount and then choose the path with the shortest number of coins.
Let's derive the partial space tree:
Where we marked the following:
- Yellow: the repeated work for an amount of
3. - Orange: the repeated work for an amount of
2. - Green: a valid solution.
This repeated work suggests that we can apply Dynamic Programming.
Solution
from typing import Dict, List
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
def dfs(curr_amount: int, memo: Dict[int, int]) -> int:
if curr_amount in memo:
return memo[curr_amount]
if curr_amount == 0:
return 0
if curr_amount < 0:
return float("+inf")
min_coins = float("+inf")
for coin in coins:
min_coins = min(min_coins, 1 + dfs(curr_amount - coin, memo))
memo[curr_amount] = min_coins
return memo[curr_amount]
num_coins = dfs(amount, {})
return num_coins if num_coins != float("+inf") else -1
Complexity
- Time:
- Space:
Where and is the size of the coins list.
Unique Paths
The problem description can be found in LeetCode.
Approach
The robot can move either down or right,
which means that we have a kind of decision tree:
at every step we can take one of the two directions.
Let's derive a partial space tree by first going down and then right:
Where we marked the following:
- Red: invalid coordinates.
- Blue: the repeated work for the coordinate
(2, 1). - Green: a valid solution.
Since we have some repeated work, we can use memoization to store some already calculated results.
Solution
from typing import Dict, Tuple
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
def dfs(row: int, col: int, memo: Dict[Tuple[int, int], int]):
if (row, col) in memo:
return memo[(row, col)]
if row == m - 1 and col == n - 1:
return 1
if not (0 <= row < m) or not (0 <= col < n):
return 0
ans = 0
ans += dfs(row + 1, col, memo)
ans += dfs(row, col + 1, memo)
memo[(row, col)] = ans
return ans
return dfs(0, 0, {})
Complexity
- Time:
- Space:
Where and are the two inputs of the function.
Partition Equal Subset Sum
The problem description can be found in LeetCode.
Approach
The problem asks us to partition the input array in two subsets, which sum up to the same value:
nums = [1, 1, 1]
It is clear that, in the case above, these two subsets do not exist. In particular, if the sum of the list is an odd number, for sure there is no solution for the problem.
So, since we know that our target is an even number,
the problem can be seen as looking for a single subset,
which sums up to target // 2 (// is the integer division in Python).
We then have the choice of either selecting an element or not.
Solution
from typing import Dict, List, Tuple
class Solution:
def canPartition(self, nums: List[int]) -> bool:
def dfs(i: int, target: int, memo: Dict[Tuple[int, int], bool]) -> bool:
if (i, target) in memo:
return memo[(i, target)]
if target == 0:
return True
if target < 0 or i >= len(nums):
return False
with_curr_val = dfs(i + 1, target - nums[i], memo)
without_curr_val = dfs(i + 1, target, memo)
ans = with_curr_val or without_curr_val
memo[(i, target)] = ans
return ans
nums_sum = sum(nums)
if nums_sum % 2 != 0:
return False
return dfs(0, nums_sum // 2, {})
Complexity
- Time:
- Space:
Where is the size of the nums list and .
Word Break
The problem description can be found in LeetCode.
Approach
A brute force approach for this problem would consist of consuming the string s by starting from any word of wordDict.
Of course, this would require common characters between the strings.
In fact, we would not complete any search with an input like:
s = "hello"
wordDict = ["foo", "bar"]
This would suggest looking any character for the strings in wordDict and
start to match them with the characters in s.
If we get a complete match for a certain string w in wordDict,
we can start to look at the wordDict again with s[:len(w)].
This is a time consuming approach because it would require to go through all the characters in s and
then all the characters of each string of wordDict.
However, we should already know about a data structure that can quickly look at prefixes: the Trie.
So, we could store all the words in wordDict in a Trie and just iterate over the strings s to look for common characters.
Solution
from typing import Dict, List, Optional
class TrieNode:
def __init__(self, is_word: Optional[bool] = False) -> None:
self.children: Dict[str, "TrieNode"] = {}
self.is_word = is_word
class Trie:
def __init__(self) -> None:
self.head = TrieNode()
def insert(self, word: str) -> None:
p = self.head
for char in word:
if char not in p.children:
p.children[char] = TrieNode()
p = p.children[char]
p.is_word = True
def search(self, word: str) -> bool:
return self._contains(word=word, match_word=True)
def startsWith(self, prefix: str) -> bool:
return self._contains(word=prefix, match_word=False)
def _contains(self, word: str, match_word: bool) -> bool:
p = self.head
for char in word:
if char not in p.children:
return False
p = p.children[char]
return p.is_word if match_word else True
class Solution:
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
def dfs(i: int, trie: Trie, memo: Dict[int, bool]) -> bool:
if i in memo:
return memo[i]
if i == len(s):
return True
if i > len(s):
return False
p = trie.head
for j in range(i, len(s)):
char = s[j]
if char not in p.children:
memo[i] = False
return memo[i]
p = p.children[char]
if p.is_word and dfs(j + 1, trie, memo):
memo[i] = True
return memo[i]
memo[i] = False
return memo[i]
trie = Trie()
for word in wordDict:
trie.insert(word)
return dfs(0, trie, {})
Complexity
- Time:
- Space:
Where:
- is the length of the list
wordList. - is the length of the longest string in
wordList. - is the length of the string
s.
K Closest Points to Origin
The problem description can be found in LeetCode.
Approach
The easiest solution would be to sort the input and than take the first k elements.
This would require time for the sorting and for selecting values.
However, we can do better!
In fact, we can use a Heap to store all the elements and
then perform k pop operations to get the closest values to origin.
Solution
import heapq
from typing import List
class Solution:
def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
heap = [(x**2 + y**2, x, y) for x, y in points]
heapq.heapify(heap)
ans = []
for _ in range(k):
_, x, y = heapq.heappop(heap)
ans.append([x, y])
return ans
Complexity
- Time:
- Space:
Where is the size of the points list.
Task Scheduler
The problem description can be found in LeetCode.
Approach
A greedy approach can be used to solve this problem.
By deriving some examples, we can prove that the best way to start would be to select the most frequent tasks and then continue with the other ones.
tasks = ["A", "A", "A", "B"]
n = 2
If we select B first we would have the sequence:
B -> A -> idle -> idle -> A -> idle -> idle -> A -> idle -> idle
However, if we select A first:
A -> B -> A -> idle -> idle -> A
Once the most frequent task is completed,
we can decrease its number of occurrences by one and
still use it for the next iteration if the number is not 0.
An efficient data structure that allows this is the Heap.
Solution
import heapq
from typing import List
class Solution:
def leastInterval(self, tasks: List[str], n: int) -> int:
counter = self.get_chars_counter(tasks)
heap = [-occ for occ in counter if occ > 0]
heapq.heapify(heap)
ans = 0
while heap:
remained_tasks = []
completed_tasks = 0
for _ in range(n + 1):
if not heap:
break
completed_tasks += 1
occ = -heapq.heappop(heap) - 1
if occ > 0:
remained_tasks.append(-occ)
for task in remained_tasks:
heapq.heappush(heap, task)
ans += completed_tasks if not heap else n + 1
return ans
def get_chars_counter(self, tasks: List[str]) -> List[int]:
m = [0] * 26
for task in tasks:
assert isinstance(task, str)
assert len(task) == 1
idx = ord(task) - ord("A")
m[idx] += 1
return m
Complexity
- Time:
- Space:
Where is the size of the tasks list.
Find Median from Data Stream
The problem description can be found in LeetCode.
Approach
Suppose to have an input like:
lst = [1, 2, 3, 4, 5]
If we divide such inputs in small and big values, we would have:
small_values = [1, 2, 3?]
big_values = [3?, 4, 5]
The median can be either in the small_values list or in the big_values one.
It will either be the last or first element of small_values and big_values, respectively.
So, if we maintain such list of values, we could easily find the median in constant time in one of the two lists.
The Heap looks like a perfect data structure we can use in this case.
We just need to maintain the balance properties between the two lists,
hence, abs(len(small_values) - len(big_values)) <= 1.
Solution
from heapq import heappop, heappush
class MedianFinder:
def __init__(self):
self.small = [] # max heap
self.large = [] # min heap
def addNum(self, num: int) -> None:
# add the value in the `max Heap`
heappush(self.small, -num)
# rearrange the values to maintain the heaps property
if self.small and self.large:
largest = -self.small[0]
smallest = self.large[0]
if largest > smallest:
_ = heappop(self.small)
heappush(self.large, largest)
self._balance_heaps()
def findMedian(self) -> float:
assert abs(len(self.small) - len(self.large)) <= 1
if len(self.small) > len(self.large):
return -self.small[0]
if len(self.large) > len(self.small):
return self.large[0]
return (-self.small[0] + self.large[0]) / 2
def _balance_heaps(self) -> None:
if len(self.small) > len(self.large) + 1:
largest = -heappop(self.small)
heappush(self.large, largest)
elif len(self.large) > len(self.small) + 1:
smallest = heappop(self.large)
heappush(self.small, -smallest)
Complexity
- addNum:
- Time:
- Space:
- findMedian:
- Time:
- Space:
Where is the number of function calls to the addNum method.
Merge k Sorted Lists
The problem description can be found in LeetCode.
Approach
A naive approach would consist in moving all the elements that belong to the k linked lists to an array.
Then, we can simply sort it.
This would require time for sorting the list and space for storing all the elements
(assuming that ).
We could improve this approach by just keeping track of the minimum element of each list:
l1 = [1, 2, 3]
l2 = [5, 6, 7]
l3 = [10, 11]
At first, we could keep min_list = [1, 5, 10], which are the minimum values for l1, l2 and l3, respectively.
The minimum of this list would be the first value of the result list.
Then, since we pick the minimum from the first list,
we should rearrange min_list based on the next value of l1, which is 2.
This results in min_list = [2, 5, 10].
Again, we can peek the first element and use it as the second element of the result list.
We can repeat this process until we have elements in our list.
Of course, the perfect data structure we can use to keep track the minimum is the Heap.
Solution
from heapq import heappop, heappush
from typing import List, Optional
class Solution:
def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
heap = []
# use the `id` to avoid to define a `heap container`,
# which needs `__lt__` to be implemented
for head in lists:
if head:
heappush(heap, (head.val, id(head), head))
head = ListNode(-1)
p = head
while heap:
_, _, node = heappop(heap)
if node.next:
heappush(heap, (node.next.val, id(node.next), node.next))
p.next = ListNode(node.val)
p = p.next
return head.next
Complexity
- Time:
- Space:
Where is the size of the nums list.
Contributors
Here is a list of the contributors who have helped to improve algo-ds.
- Marco. The author of the website.
- schrodingercatss:
- (05/08/2024) Fix typo in Monotonic Stacks and Queues.
- (05/08/2024) Use the proper snippet in Union by Rank + Path Compression.
- lentil32:
- (04/09/2024) Include
addfunction in Sets. - (04/09/2024) Use proper snippet in Iterative Binary Search.
- (04/09/2024) Fix typo in Analyze Recursive Functions.
- (04/09/2024) Fix typo in Arrays.
- (21/10/2024) Fix typo in Minimum Window Substring.
- (21/10/2024) Fix substring length calculation in Minimum Window Substring.
- (04/09/2024) Include
If you feel you are missing from this list, check the Contribute section.